PHY294H - More on Lecture 1

Coulomb's law

Force between two charges The starting point in electrostatics is Coulomb's law, which gives the force between two stationary charges,

$$\vec{F} = k {Q q \over r^2} \hat{r} = k {Q q \over r^3} \vec{r}$$ (1)

- Q, q are stationary charges. Their units are coulombs (C)
- $\hat{r}$ is a unit vector along the line between the two charges.
- $\vec{r}$ is the vector distance between the two charges.
- $k = 9\times 10^{9} Nm^2/C^2 = 9\times 10^{9} kg m^3/C^2s^2$.
- $k = 1/4\pi\epsilon_0$. $\epsilon_0$ is the permittivity of free space.

Gravitational force law

$$\vec{F_G} = - G {M m \over r^2} \hat{r}$$ (2)

- $G = 6.67\times 10^{-11} N m^2/kg^2$. The gravitational force is much weaker than the electostatic force.

Example

Find the ratio of the magnitudes of the gravitational and electrostatic forces between two protons.

Solution The ratio of the magnitudes of the gravitational and electrostatic forces is,

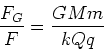$${F_G\over F} = {G M m\over k Q q}$$ (3)

For two protons, we have, $M=m=1.67\times10^{-27}kg$ and $Q = q = 1.6\times 10^{-19}C$. Plugging these numbers yields,

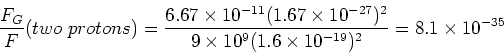$${F_G\over F}(two\ protons) = {6.67\times 10^{-11} (1.67\time... ... 9\times 10^{9} (1.6\times 10^{-19})^2} = 8.1 \times 10^{-35}$$ (4)

Most charge is ``bound''

Due to the fact that the force between charges is so large, most charge is bound. That means that negative and positive charges are close to each other in regions where the total charge is almost zero. This raises the question. Why don't charges self destruct by crashing into each other and annihilating? The answer is in quantum mechanics, which provides an understanding of how atoms are stable. Atoms are composed of electrons orbiting the nuclei which contains the protons. This provides a stable configuration of bound charges. Within electrostatics bound charges still form dipoles. There are many more charge dipoles than there are free charges. Many electrostatic effects are due to dipoles rather than free charges, so we need to understand dipoles well.

Force between many charges - superposition

Force on a charge q due to many other charges, Q₁, Q₂, ...Q_nis just the sum of the forces due to each of these charges, ie.

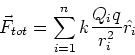$$\vec{F}_{tot} = \sum_{i=1}^n k {Q_i q \over r_i^2} \hat{r_i}$$ (5)

This looks simple, but of course it is a vector sum, so the math can get messy. r_i is the distance between charge iand the charge q. $\hat{r}_i$ is a unit vector along the vector which goes from charge q to charge Q_i.

Example- discrete charge distribution

Consider three charges located (and fixed) at (x,y) positions $\vec{r}_1=(0,0),\ \vec{r}_2=(2,0),\ \vec{r}_3=(0,2)$ (in meters) and having charges $q_1=q_2=2nC,\ q_3=-3nC$. Find the force acting on charge q₃ due to the other two charges.

Solution

We need to treat the force as a vector. In this problem the best way to treat the force is to resolve the Coulomb force between each pair of charges into its x-components and it y-components. The charges form an isosceles right-angle triangle, with charge q₁ lying at the right-angle corner. The other angles in the triangle are 45^o. The x-component of the force on charge q₃ is given by,

$$f_x = k {q_1 q_2\over r_{12}^2} cos(45) + 0$$ (6)

The y-component of the force on charge q₃ is given by,

$$f_y = k {q_1 q_2\over r_{12}^2} sin(45) + k {q_1 q_3\over r_{13}^2}$$ (7)

The principle of superposition also applies when there is a continuous distribution of charge. For example charge distributions on rods, discs, spheres etc. However when treating these distibutions, the sum in Eq. (5) becomes an integral. In treating these problems, we define a small element of charge dQ. This is the amount of charge in a small part of the continuous charge distribution. We shall consider three cases:

- Lines: Then $dQ = \lambda dx$, where $\lambda$ is the linear charge density.

- Surfaces: Then $dQ = \sigma dA$, where $\sigma$ is the surface charge density.

- Volumes: Then $dQ = \rho dV$, where $\rho$ is the volume charge density.