Suggested reading for Lecture 11: FGT pp691-706
Continuous distributions of charge
Uniform ring
Consider a thin uniform ring of charge density ![]() and radius R.
Consider that the ring is centered at the origin and lies in the
x-y plane. Find the electric potential at position z
on the z-axis. From this electric potential confirm the
result we have before for the electric field at this point
ie.
Ez(z) = kQz/(R2+z2)3/2.
and radius R.
Consider that the ring is centered at the origin and lies in the
x-y plane. Find the electric potential at position z
on the z-axis. From this electric potential confirm the
result we have before for the electric field at this point
ie.
Ez(z) = kQz/(R2+z2)3/2.
Solution
Break the ring up into angular segments, with the
angle ![]() going from 0 to
going from 0 to ![]() as it goes
around the ring. The amount of charge in a small
segment of the ring
as it goes
around the ring. The amount of charge in a small
segment of the ring
![]() .
The
distance from this small element of charge to the
position z is
r=(z2+R2)1/2. The contribution
of this small element of charge to the total
potential at z is kdQ/r. We find the total
contribution by integrating,
.
The
distance from this small element of charge to the
position z is
r=(z2+R2)1/2. The contribution
of this small element of charge to the total
potential at z is kdQ/r. We find the total
contribution by integrating,
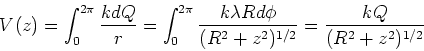 |
(1) |
Uniform disc
Consider a thin uniform disc of charge density ![]() and radius a.
centered at the origin and lying in the
x-y plane. Find the electric potential at position z
on the z-axis and from this electric potential find
the electric field at this point.
and radius a.
centered at the origin and lying in the
x-y plane. Find the electric potential at position z
on the z-axis and from this electric potential find
the electric field at this point.
Solution
Break the disc up into uniform rings of charge, with each ring
having width dR. The charge in each ring is
![]() .
The potential due to a ring of charge is given in Eq. (1)
except we need to make the substitution
.
The potential due to a ring of charge is given in Eq. (1)
except we need to make the substitution
![]() .
Then we need to integrate from 0 to a, that is,
.
Then we need to integrate from 0 to a, that is,
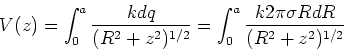 |
(2) |
| (3) |
| (4) |
Now we look at two cases that seem strange. The infinite
sheet and the infinite rod of charge. In these cases
we do not take the limit of integration to infinity.
An infinite sheet of charge
Consider an infinite sheet of charge density ![]() lying in the
x-y plane. We want to find the electric potential at a
position z above this sheet of charge.
The electric field due to this sheet of charge is
lying in the
x-y plane. We want to find the electric potential at a
position z above this sheet of charge.
The electric field due to this sheet of charge is
![]() .
Therefore the electric potential is,
.
Therefore the electric potential is,
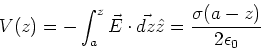 |
(5) |
An infinite rod of charge
From Gauss' law, the electric field outside an infinite uniform rod
of charge density ![]() is given by,
is given by,
| (6) |
| (7) |
Sharp metal objects
Sharp metal tips are surprisingly important. From lightning rods to tunnelling tips in scanning microscopes we use sharp metals tips to control and/or enhance electric fields. Due to the fact that the electric field inside a conductor is zero, if there is no current flow, a conductor in an external electric field causes strong deformations of the electric field lines and the equipotential lines. These deformations are particularly important near sharp metal tips where the electric field is strongly enhanced. For this reason, conducting metal rods are used for lightning protection and as atomic scale probes of materials.
As a simple example, consider two metal spheres of radii r1 and r2 respectively.
Place these spheres well apart so that they do not polarize
each others charge distribution significantly. Now connect the
two metal spheres using a conducting wire. Since the metals
are conducting, and when there is no current flowing, the
two spheres are at the same potential, e.g. about 500kV if
we use our Van de Graaff generator. Now we demonstrate that
by using the potential and the radii r1 and r2, we
can make a electric field amplifier. Let the charge on
sphere one be Q1 and the charge on sphere two be Q2. Then
we have,
| (8) |
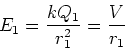 |
(9) |
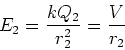 |
(10) |
| (11) |
The strong electric field enhancement near the small metal sphere in
the above example is a simple illustration of a very general effect.
An important more general result
is that a sharp metal object aligned along the direction of
a uniform electric field has a very strong electric field
enhancement at its tips. If the sharp metal object has
length a and radius of curvature r at its tip, then
it can be shown that the electric field enhancement at the
tip is given by,
| (12) |