PHY294H - Lecture 11

What is a capacitor?

Any two pieces of metal, which are separated by an insulator, have a capacitance. The capacitance of the two pieces of metal tells us how much voltage we need to apply in order to place a charge Q on one of the pieces of metal and a charge -Q on the other. That is,

Q = CV (1)

Note that when we talk of capacitance we are talking about equal and opposite charges on the two pieces of metal. V is the potential difference between the two pieces of metal. The first question we should ask is why Eq. (1) should be correct. That is, why should the voltage be linearly proportional to the charge? To understand this, consider the way in which the potential is defined. It is the integral of the electric field. The electric field is proportional to the charge, so if we double the charge, we double the electric field and hence we double the potential. Thus the charge is proportional to the potential. Now we want to find the constant of proportionality, which we call the capacitance. The units of capacitance are 1 Coulomb/1 Volt. However capacitance is such an important quantity that it is given a unit of its own, the Farad (F).

Calculating capacitance

Parallel plates

Consider two square parallel plates with charge Q (positive Q on one plate and negative Q on the other). The plates are separated by distance d and have area A = L². Consider L>>d, so we can approximate the magnitude of the electric field between the plates by $E = \sigma/\epsilon_0$. The potential difference between the places is

$$V = E d = {\sigma d\over \epsilon_0} = {Q d \over \epsilon_0 A}$$ (2)

Comparing Eqs. (1) and (2), we see that for parallel plates,

$$C = {\epsilon_0 A\over d}$$ (3)

Coaxial cable

A co-axial cable consists of an inner conducting rod of radius a and an outer conducting cylindrical shell of radious b. Here we assume that between these two radii there is air, however in reality there is a very good insulator. We want to find the capacitance of this system, per unit length. Assuming that the rod and outer shell have equal and opposite charge densities $\lambda$, the magnitude of the electric field in the regime a<r<b is given by,

$$2\pi r L E(r) = {\lambda L\over \epsilon_0}$$ (4)

The voltage is found by integration,

$$V_{ab} = -\int_b^a \vec{E}\cdot \vec{dr} = -\int_b^a {\lambd... ... 2\pi \epsilon_0 r} = {\lambda \over 2\pi \epsilon_0} ln(b/a)$$ (5)

comparing this with Eq.(1), we find,

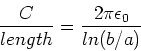$${C\over length} = { 2\pi \epsilon_0 \over ln(b/a)}$$ (6)

An isolated sphere

Since an isolated sphere, of radius R, has a well defined potential with respect to infinity, we can also calculate the capacitance of the isolated sphere with respect to infinity. We have,

$$V = {k Q\over R}$$ (7)

Comparing this with Eq. (1), we find,

$$C = {R\over k}$$ (8)

The energy stored in a capacitor

When we talk of the energy stored in a capacitor, we are refering to the electrostatic potential energy. The stored electrostatic potential energy is equal to the work done in separating the charges +Q and -Q which are on the two metal parts of the capacitor. As in the case of setting up a distribution of point charges, we start with the capacitor with no charges on the plates. For each small element of positive charge, dq, that we move from the negative plate to the positive plate, we increase the potential energy by dU = V(q) dq. Since V(q) = q/C, the potential energy change is dU = qdq/CWe continue this process until the total charge Q is on the capacitor. The total potential energy is then,

$$U = \int dU = \int_0^Q {qdq \over C} = {Q^2\over 2C} = {1\over 2} CV^2 = {1\over 2} QV$$ (9)

Note that the amount of energy that can be stored in a capacitor is relatively small. That is why we don't see capacitors used for energy storage in cars and electrical devices. However the advantage of capacitors is that that have a fast response time, the charge can move off and onto the capacitor plates very rapidly. This is why capacitors are used for high power pulsed lasers and other applications requiring short high current pulses.

The energy in the electric field

An important way of thinking about the energy stored in a capacitor is that the energy actually goes into establishing the electric field. This is evident in the case of the parallel plate capacitor, where we can use V=Ed to write,

$$U = {1\over 2} C V^2 = {1\over 2} {\epsilon_0 A \over d} E^2d^2 = {1\over 2} \epsilon_0 E^2 volume$$ (10)

where volume = A d is the volume between the two parallel plates. This allows us to define the energy density,

$$u = {U \over volume} = {1\over 2} \epsilon_0 E^2$$ (11)

which is the general result for the energy stored in the electric field, even if the electric field is non-uniform. In the case of a non-uniform field, we would need to integrate the energy density over the volume in which the electric field is significant.