PHY294H - Lecture 12

Recommended problems for Lecture 12: 26.6, 26.26, 26.37 26.45
Recommended reading for Lecture 13: Chap. 26

Now that we have the defined what a capacitor is, we can begin our study of circuits. We have seen that to make a capacitor all we need is two pieces of metal. In power circuits we need large capacitors so parallel plates are used (they are often wrapped into cylinders), with a good dielectric material between them. In integrated circuits metal films are separated by insulating layers in the fabrication process. In addition to the capacitors that we want, circuit designers often have to deal with stray capacitance, that is capacitors that we don't want and can't get rid off. In circuit analysis it is often possible to reduce a complicated looking circuit to a simpler form. We will learn how to do this for capacitors. Many complicated circuits can be reduced if we know how to reduced combinations which are in series or in parallel.

Capacitors in series and parallel

Series combination

When capacitors are combined in series, the charge on each plate(piece of metal) has the same magnitude. If there are n capacitors in series, each may have a different voltage across its plates. Let's call the voltage across the i^th capacitor V_i. We want to combine the n capacitors which are connected in series into one capacitor which has capacitance C_series. If this is possible, this ``effective capacitor'' also has charge magnitude Q on its places. The voltage, V, across the plates of this effective capacitor then should satisfy,

Q = C_series V = C_series(V₁+V₂ +....V_n) (1)

Each of the individual capacitors also obeys V_i = Q/C_i. Using this in Eq. (1), we find,

$${Q\over C_{series}} = V = {Q\over C_1}+{Q\over C_2} +....{Q\over C_n}$$ (2)

From this we find the result for a series combination of capacitors,

$${1\over C_{series}} = {1\over C_1}+{1\over C_2} +....{1\over C_n}$$ (3)

Parallel combination

When capacitors are combined in parallel they have the same voltage across each capacitor. Thus we can write

Q = C_parallel V = Q₁+Q₂+...Q_n (4)

This implies that,

Q = C_parallel V = C₁V+C₂V+...C_nV (5)

From this we see that for the parallel combination,

C_parallel = C₁+C₂+...C_n (6)

Example

Consider a parallel combination of $C_1 = 10\mu F$ and $C_2=6\mu F$ which is in series with two capacitors $C_3 = 5\mu F$ and $C_4=2\mu F$.

Parallel combination

$$C_p = C_1 + C_2 = 16\mu F$$ (7)

Series combination

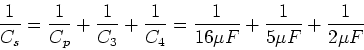$${1\over C_s} = {1\over C_p} + {1\over C_3} + {1\over C_4} = {1\over 16\mu F} + {1\over 5\mu F} + {1\over 2\mu F}$$ (8)

This gives,

$$C_s = {80 \over 61} \mu F$$ (9)

Dielectric materials

So far, we have discussed the electric field in vacuum. That is, we have not even included the effect of air. However air does not alter the electric field much, so our previous conclusions apply almost unaltered to air. However if we place charges inside a material, either a liquid like water or a solid material then there can be important changes in the electric field and capacitance as compared to the same charges in air. Actually we have already seen this. The behavior of conductors is very different than the behavior of air. However we now want to consider insulating materials, which we now call "dielectrics'' when they are used to modify electric fields or when they are used inside a capacitor. For the purposes of this course we shall only need one formula to describe how to treat the effect of a dielectric material on electric fields and capacitance. We make the replacement,

$$\epsilon_0 \rightarrow \epsilon = \kappa \epsilon_0$$ (10)

in all of our electrostatics formulae. Every dielectric material has a value for $\kappa$, with $\kappa \approx 1$ for air, $\kappa =12$for silicon and $\kappa = 80$ for pure water. $\kappa \rightarrow \infty$ for conductors. The capacitance of a parallel place capacitor is,

$$C = {\kappa \epsilon_0 A \over d}$$ (11)

Thus the higher the value of $\kappa$, the ``better'' it seems the capacitor is. However this is not the whole story. If current flow occurs, then the charge separation is lost. Each material has a threshold electric field at which it ``fails''. The threshold electric field in air is approximately $E_c = 3\times 10^6V/m$. However for metals it is E_c = 0 as current flow occurs as soon as an electric field is applied. For water the threshold field is very low because water usually contains dissolved ions which can move under the influence of an electric field. Dielectric materials like ceramics or polymers have E_c > E_c(air)so they enable much higher charge storage than parallel plates with air gaps.