For the next three lectures we shall discuss direct current
circuits. Our work on electrostatics enables us to understand
what a capacitor is and our work on the resistivity of materials
enables us to understand the processes which are occuring
in resistors. We also need to have a source of applied
current and voltage. We could use capacitors for this
purpose, but they are rather poor for storing energy, so
they aren't usually used, except in cases where a very large,
but very short current pulse is required. Our voltage sources
are usually chemical in origin, as are most of the
stored energy devices in technology. They are called a
battery, a DC voltage source or an electromotive force (emf).
In the ideal case, which we shall almost always
use, the emf is assumed to have a fixed potential, and that
it is able to deliver an unlimited amount of current. The
symbol we shall use for source emf is ![]() .
In our circuits
the emf
.
In our circuits
the emf ![]() will be fixed, however the current that it supplies depends
on the load in the circuit. The load in the circuit is the
set of resistors and capacitors to which the emf is supplying current.
Our task is to figure out the transient and steady state current
supplied to the load for a variety of possible circuits.
will be fixed, however the current that it supplies depends
on the load in the circuit. The load in the circuit is the
set of resistors and capacitors to which the emf is supplying current.
Our task is to figure out the transient and steady state current
supplied to the load for a variety of possible circuits.
An emf and a resistor
An ideal emf supplies a voltage ![]() .
Let us assume that
the positive terminal of the emf is at voltage V1 and
is attached by a zero resistance
wire to one terminal of a resistor. The negative terminal of
the emf is connected, by a zero resistance wire, to the other terminal
of the resistor. Since the connecting wires have zero resistance, there
is no voltage drop across them. Therefor the voltage at the
positive end of the resistor is the same as that of the
positive terminal of the emf. Similarly the potential
at the negative end of the resistor is the same as that of the
negative terminal of the emf. The voltage drop across the
resistor is thus
.
Let us assume that
the positive terminal of the emf is at voltage V1 and
is attached by a zero resistance
wire to one terminal of a resistor. The negative terminal of
the emf is connected, by a zero resistance wire, to the other terminal
of the resistor. Since the connecting wires have zero resistance, there
is no voltage drop across them. Therefor the voltage at the
positive end of the resistor is the same as that of the
positive terminal of the emf. Similarly the potential
at the negative end of the resistor is the same as that of the
negative terminal of the emf. The voltage drop across the
resistor is thus ![]() .
From Ohm's law we have V=IR,
so we have,
.
From Ohm's law we have V=IR,
so we have,
| (1) |
Series and parallel combinations of resistors
Series combination
Consider a series combination of resistors R1, R2, ..., Rn.
We apply an emf ![]() .
We want to replace this series combination
by one resistor
Rseries. Since the same current must
flow through all of the resistors (current conservation) and
using Ohm's law, we have,
.
We want to replace this series combination
by one resistor
Rseries. Since the same current must
flow through all of the resistors (current conservation) and
using Ohm's law, we have,
| (2) |
| Rseries = R1 + R2 + R3 + .... + Rn | (3) |
Example
The case above of an emf ![]() with resistance r and load resistance Rleads to an effective emf R+r which is connected in series with the
ideal emf
with resistance r and load resistance Rleads to an effective emf R+r which is connected in series with the
ideal emf ![]() .
The current flowing in the circuit is then
.
The current flowing in the circuit is then
![]() .
The voltage drop across the internal resistance is
.
The voltage drop across the internal resistance is
| (4) |
Parallel combination
Consider a parallel combination of resistors R1, R2, ...., Rn.
We want to replace this parallel combination by one resistor
Rparallel.
To do this, note that the voltage across each of these resistors
must be the same and it must be equal to ![]() .
The current supplied
to the resistance satisfies
.
The current supplied
to the resistance satisfies
![]() .
This current must be
equal to the sum of the currents passing through the n parallel resistors,
.
This current must be
equal to the sum of the currents passing through the n parallel resistors,
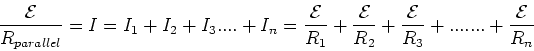 |
(5) |
 |
(6) |
General multiloop circuits
The series and parallel combination laws for resistance
and for capacitance are very useful. However they are not the
whole story as there are circuits which cannot be reduced using
those rules alone. Now we will learn how to solve for the
current flow everywhere in multiloop circuits and
the voltage drop across all of the
resistors and capacitors in our circuits. To carry out this
analysis we shall use Kirchhoff's laws:
Kirchhoff's junction rule
The sum of the currents which enter a junction must
equal the sum of the currents which leave that junction.
(This is the same as current conservation)
Kirchhoff's loop rule
The sum of the voltage drops around a closed loop must be zero.
(This is the same are requiing that if we go around
a closed loop the amount we go up in potential
must be equal to the amount we go down in potential)