


Next: About this document ...
PHY294H - Lecture 17
Capacitor/Resistor networks
Kirchhoff's laws still apply and are the basis for
analysis of RC circuits. In analysing these circuits
we need to relate the charge on the capacitors
to the current flow into the capacitor. The
relationship we need is simply i = dQ/dt. This
is combination with Kirchhoff's laws enable us
to solve RC circuits. We shall be interested in the
way that capacitors in a circuit charge and discharge.
We shall also be interested in the long time behavior
(steady state) in which each capacitor has reach
a final charge state. To study charging, we
will close a switch in the circuit and will
analyse what happens as charge either flows
onto or off of the capacitors.
A resistor and capacitor in series
Consider Kirchhoff's loop law for a capacitor, C, resistor R and
an emf 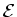 in series. At long times, this circuit carries
no current and the emf is dropped across the capacitor.
The circuit is only interesting if we have a switch in the circuit
which we can open and close as we wish. Analysis
of the time dependence of the current in the circuit and the
charge across the capacitor is a study of transients.
in series. At long times, this circuit carries
no current and the emf is dropped across the capacitor.
The circuit is only interesting if we have a switch in the circuit
which we can open and close as we wish. Analysis
of the time dependence of the current in the circuit and the
charge across the capacitor is a study of transients.
Charging a capacitor
Consider placing a switch in the circuit and
the situation in which the capacitor initially
has charge
Q(t=0) = 0. We close the switch at
t=0 and the capacitor begins to charge.
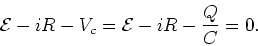 |
(1) |
In order to proceed we use the relation between current
and charge, ie. i = dQ/dt. From this we find,
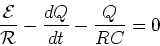 |
(2) |
In the steady state
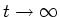 ,
i = dQ/dt=0 and
,
i = dQ/dt=0 and
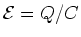 .
The time dependence of the charging of the capacitor is
given by the solution to Eq. (2), which is,
.
The time dependence of the charging of the capacitor is
given by the solution to Eq. (2), which is,
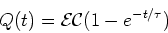 |
(3) |
where the time constant 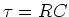 .
Note that Q(0) = 0 and that
.
Note that Q(0) = 0 and that
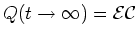 .
The current as a function of time is given by,
.
The current as a function of time is given by,
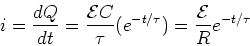 |
(4) |
Discharging a capacitor
Now consider a capacitor which has charge Q0 in a circuit with
a resistor and an open switch. The switch is closed at t=0.
Find the current in the circuit and the charge on the capacitor as
a function of time. Kirchhoff's loop law gives,
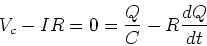 |
(5) |
The solution to this equation is,
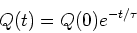 |
(6) |
The current in the circuit is,
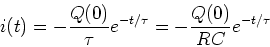 |
(7) |
Energy storage and dissipation in an RC circuit
In the charging process above, the energy supplied
by the emf (battery) is
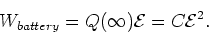 |
(8) |
half of this energy is stored in the capacitor and half of
this energy is dissipated in the resistor.
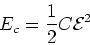 |
(9) |
The energy dissipated in the resistor is
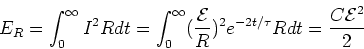 |
(10) |
FGT 28.59
Consider an emf 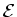 in parallel with a resistor R2 and
in parallel with a series combination of a resistor R1 and
a capacitor C. A switch is placed near the emf. At times
t<0 the capacitor is uncharged and the switch is open. At
t=0 the switch is closed. Find an expression for the
current through the battery, I(t), as a function of time and
the charge on the capacitor Q1(t), also as a function of time.
in parallel with a resistor R2 and
in parallel with a series combination of a resistor R1 and
a capacitor C. A switch is placed near the emf. At times
t<0 the capacitor is uncharged and the switch is open. At
t=0 the switch is closed. Find an expression for the
current through the battery, I(t), as a function of time and
the charge on the capacitor Q1(t), also as a function of time.
Kirchhoff's junction law gives,
where I1 and I2 are the currents through resistors
R1 and R2 respectively. Kirchhoff's loop law gives,
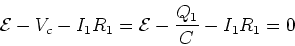 |
(12) |
and,
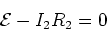 |
(13) |
For times t<0, there is no current in the circuit as the
switch is open. At time t=0 the switch is closed. At that
time, there is no charge on the capacitor, so there is no
voltage across the capacitor. Therefore the circuit
acts like a parallel combination of resistors R1
and R2. We thus have,
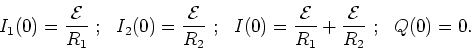 |
(14) |
At long times, the capacitor is fully charged and
we have,
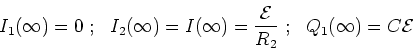 |
(15) |
To find the time dependence of the current I1 we use
I1 = dQ1/dtin Eq. (12). This yields,
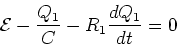 |
(16) |
This has the solution,
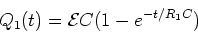 |
(17) |
The current I1(t) is then,
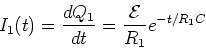 |
(18) |
Using Kirchhoff's junction rule, we then find,
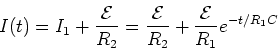 |
(19) |



Next: About this document ...
Phil Duxbury
2002-09-24
![]() in series. At long times, this circuit carries
no current and the emf is dropped across the capacitor.
The circuit is only interesting if we have a switch in the circuit
which we can open and close as we wish. Analysis
of the time dependence of the current in the circuit and the
charge across the capacitor is a study of transients.
in series. At long times, this circuit carries
no current and the emf is dropped across the capacitor.
The circuit is only interesting if we have a switch in the circuit
which we can open and close as we wish. Analysis
of the time dependence of the current in the circuit and the
charge across the capacitor is a study of transients. ![]() in parallel with a resistor R2 and
in parallel with a series combination of a resistor R1 and
a capacitor C. A switch is placed near the emf. At times
t<0 the capacitor is uncharged and the switch is open. At
t=0 the switch is closed. Find an expression for the
current through the battery, I(t), as a function of time and
the charge on the capacitor Q1(t), also as a function of time.
in parallel with a resistor R2 and
in parallel with a series combination of a resistor R1 and
a capacitor C. A switch is placed near the emf. At times
t<0 the capacitor is uncharged and the switch is open. At
t=0 the switch is closed. Find an expression for the
current through the battery, I(t), as a function of time and
the charge on the capacitor Q1(t), also as a function of time.