Recommended problems for Lecture 19: 29.47, 29.55, 29.54
Recommended reading: pp 790-798.
Two remarks:
(i) Magnetic field lines come out of the N pole and go into the S pole.
(ii) North geographic pole is close to the South
magnetic pole.
A current carrying wire in a magnetic field
We have learned that a moving charge experiences
a force which is equal to
![]() .
Since current flow corresponds to moving charges, a
current carrying wire should also experience a force
when it is placed in a perpendicular magnetic field. The force on
a straight wire carrying current I is easily derived from
the magnetic force. The velocity which contributes to
current is the drift velocity, vd.
The current density is given by nq q vd and the
current is
I= jA = A nqqvd. The force on each charge is then,
on average,
.
Since current flow corresponds to moving charges, a
current carrying wire should also experience a force
when it is placed in a perpendicular magnetic field. The force on
a straight wire carrying current I is easily derived from
the magnetic force. The velocity which contributes to
current is the drift velocity, vd.
The current density is given by nq q vd and the
current is
I= jA = A nqqvd. The force on each charge is then,
on average,
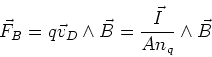 |
(1) |
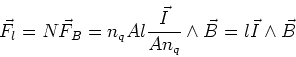 |
(2) |
| (3) |
If we have a wire which
changes direction, then the total force on the
wire is a vector sum of terms of the form ![]() .
We have to integrate these terms over the length of the
wire, that is
.
We have to integrate these terms over the length of the
wire, that is
| (4) |
Long straight wire
If we place a long straight wire of length L and at angle ![]() to
a constant magnetic field (B), then the force on the
wire is given by,
to
a constant magnetic field (B), then the force on the
wire is given by,
| (5) |
FGT 29.45
The magnetic force on the wire is ILB down the page.
At equilibrium this is equal to the force in the springs,
F = 2 k y. Equating these two forces, we have,
| y = ILB/2k | (6) |
Magnetic force on current loops
Current loop in a magnetic field
Consider a rectangular loop, which has its long
sides with length b and its short sides with
length a, and which carries current I.
This loop is mounted on an insulating axis of
rotation. This axis is perpendicular to the
direction of the magnetic field, which is
assumed to be uniform. We want to find the
force on this loop as a function of the
angle between the loop and the direction of the magnetic
field. We take the angle between the normal
to the loop and the direction of the magnetic field
to be ![]() and we define
and we define
![]() .
Let us take the long sides of the loop to be
parallel to the axis of rotation and the short axes of the
loop to be perpendicular to the axis of rotation. The first
result is that if the magnetic field is constant, there
is no net force on the loop. We demonstrate this by
treating first the two long sides of the loop:
.
Let us take the long sides of the loop to be
parallel to the axis of rotation and the short axes of the
loop to be perpendicular to the axis of rotation. The first
result is that if the magnetic field is constant, there
is no net force on the loop. We demonstrate this by
treating first the two long sides of the loop:
The force on each of these sides is F = I b B and
F=-IbB. The forces on the short sides is
![]() and
and
![]() .
There is thus no net force on the
loop.
.
There is thus no net force on the
loop.
Altough there is no net force on the
loop, there is a net torque. The torque is defined as,
| (7) |
| (8) |
FGT 29.54
In this problem we cannot use ![]() because the
current does not go around the loop. The dipole
moment formula only works for current loops.
Instead, this is a current divider.
The current V1=V2, so
I1R1 = I2R2.
We also have I=I1+I2, so the currents I1 and I2 are given by,
because the
current does not go around the loop. The dipole
moment formula only works for current loops.
Instead, this is a current divider.
The current V1=V2, so
I1R1 = I2R2.
We also have I=I1+I2, so the currents I1 and I2 are given by,
| (9) |
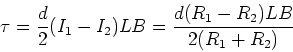 |
(10) |