Example - uniform ring of charge
Consider a thin perfectly circular ring centered at the origin,
with radius R, lying in the x-y plane and being
uniformly charged with linear charge density ![]() .
Find the force on a charge q placed at position,
.
Find the force on a charge q placed at position,
![]() .
.
Solution
By symmetry, the x and y components of the force on the charge are
zero. We are thus left with the task of calculating the z-component.
The distance, r, from the charge to any point on the ring is given by,
| r2 = R2 + z2 | (1) |
| (2) |
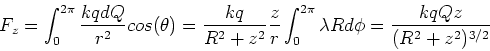 |
(3) |
The electric field
The electric field is a very important concept
in all of electromagnetism.
At first it seems like it is the same as
Coulomb's law. In fact it is. However it is a much
better way of thinking about electrostatic forces.
Definition: Electric field
The electric field at a point ![]() due to
a charge distribution is defined in terms of the
force on a positive test charge, q, placed at
position
due to
a charge distribution is defined in terms of the
force on a positive test charge, q, placed at
position ![]() .
The precise definition is,
.
The precise definition is,
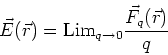 |
(4) |
Superposition works for the electric field (Obviously!!)
From the definition of the electric field, we write
Coulomb's law as,
| (5) |
In a similar way, the electric field due to a distribution of
discrete charges is given by,
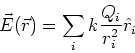 |
(6) |
Example- discrete charge distribution
Consider three charges located (and fixed) at (x,y) positions
![]() (in meters) and having charges
(in meters) and having charges
![]() .
Find the force acting on charge q3 due
to the other two charges. What is the electric field at position
.
Find the force acting on charge q3 due
to the other two charges. What is the electric field at position ![]() due to charges q1 and q2?
due to charges q1 and q2?
Solution
We need to treat the force as a vector. In this problem
the best way to treat the force is to resolve the Coulomb
force between each pair of charges into its x-components
and it y-components. The charges form an isosceles right-angle
triangle, with charge q1 lying at the right-angle corner.
The other angles in the triangle are 45o.
The x-component of the force on charge q3 is given by,
| (7) |
| (8) |
| (9) |
Example - uniform ring of charge
Find the electric field for the thin charge ring discussed above.
Solution
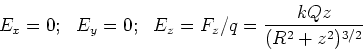 |
(10) |
Electric dipole
An electric dipole consists of two charges of equal and opposite sign (-q,q), separated by distance L. As we shall see below, the electric dipole moment is the product p=qL, which measures the strength of the dipole. A vector direction is also assigned to the electric dipole moment, and this direction is chosen to be from the negative charge to the positive charge. Consider an electric dipole, centered at the origin and lying along the x-axis, with the positive charge at x-position, L/2. Find the electric field due to this dipole at any point in the x-y plane. Notice that this is the general solution as there is rotational symmetry about the x-axis.
At any point P located at (x,y) in the x-y plane we define
r1 to be the distance from the positive charge to the point
(x,y),
| (11) |
| (12) |
![\begin{displaymath}\vec{E}(x,y) = kq[{\hat{r}_{1P} \over r_{1p}^2} - {\hat{r}_{2P} \over r_{2p}^2} ]
\end{displaymath}](img23.gif) |
(13) |
| (14) |
| (15) |
| (16) |
Electric field lines
1. At each point along an electric field line, the force on a positive test charge is in a direction tangent to the field line at that point.
2. The density of lines at any point in space is proportional to the magnitude of the electric field at that point.
3. Electric field lines begin and/or end at charges, or they continue off to infinity. i.e. they do not begin or end in free space.
4. Electric field lines do not cross.
Very important special case: conductors
1. If there is no current flowing, then the electric field
is zero, ![]() ,
inside a conductor.
,
inside a conductor.
2. If there is no current flowing, then at the surface of a conductor,
the electric field is normal to the surface of the conductor.