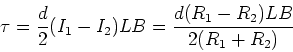Next: About this document ...
Lecture 20 - PHY294H
Magnetic dipole
We found that the torque on current loops could be
written in the form,
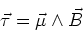 |
(1) |
where 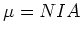 for a N-loop coil of
area A carrying current I. The
magnetic dipole direction is given by the
right hand rule with the fingers curling
in the direction of the current flow
and the thumb giving the direction of the
magnetic moment. The torque is zero when the
magnetic dipole is aligned or anti-aligned
with the magnetic field,
while the torque is a maximum when the magnetic
dipole is perpendicular to the magnetic field.
As in the case of electric dipoles, it is
easy to show that the energy of the magnetic
dipole is given by,
for a N-loop coil of
area A carrying current I. The
magnetic dipole direction is given by the
right hand rule with the fingers curling
in the direction of the current flow
and the thumb giving the direction of the
magnetic moment. The torque is zero when the
magnetic dipole is aligned or anti-aligned
with the magnetic field,
while the torque is a maximum when the magnetic
dipole is perpendicular to the magnetic field.
As in the case of electric dipoles, it is
easy to show that the energy of the magnetic
dipole is given by,
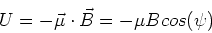 |
(2) |
where 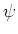 is the angle between the direction
of the magnetic field and the direction of the
magnetic moment. If
is the angle between the direction
of the magnetic field and the direction of the
magnetic moment. If 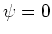 the moment
and the field are aligned,
the moment
and the field are aligned,
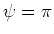 when
they are anti-aligned.
when
they are anti-aligned.
Example 29.6
A current loop of magnetic moment 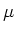 in a constant field, B, and moment of
inertia about its center, IM. It
is displaced by a small
angle
in a constant field, B, and moment of
inertia about its center, IM. It
is displaced by a small
angle 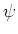 from the aligned state.
If the current loop is released at t=0 find
the subsequent motion of the loop.
from the aligned state.
If the current loop is released at t=0 find
the subsequent motion of the loop.
The torque on the loop is
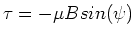 .
This torque leads to an angular acceleration
.
This torque leads to an angular acceleration
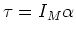 .
Equating these two expressions, we have,
.
Equating these two expressions, we have,
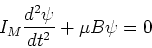 |
(3) |
where we have used the small angle approximation
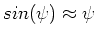 .
This has solution,
.
This has solution,
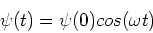 |
(4) |
where
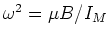 .
.
FGT 29.54
In this problem we cannot use 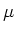 because the
current does not go around the loop. The dipole
moment formula only works for current loops.
Instead, this is a current divider.
The current V1=V2, so
I1R1 = I2R2.
We also have I=I1+I2, so the currents I1 and I2 are given by,
because the
current does not go around the loop. The dipole
moment formula only works for current loops.
Instead, this is a current divider.
The current V1=V2, so
I1R1 = I2R2.
We also have I=I1+I2, so the currents I1 and I2 are given by,
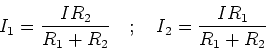 |
(5) |
The torque on the loop is then given by,
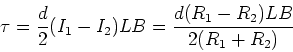 |
(6) |



Next: About this document ...
Phil Duxbury
2002-10-08
![]() in a constant field, B, and moment of
inertia about its center, IM. It
is displaced by a small
angle
in a constant field, B, and moment of
inertia about its center, IM. It
is displaced by a small
angle ![]() from the aligned state.
If the current loop is released at t=0 find
the subsequent motion of the loop.
from the aligned state.
If the current loop is released at t=0 find
the subsequent motion of the loop.
![]() .
This torque leads to an angular acceleration
.
This torque leads to an angular acceleration
![]() .
Equating these two expressions, we have,
.
Equating these two expressions, we have,
![]() because the
current does not go around the loop. The dipole
moment formula only works for current loops.
Instead, this is a current divider.
The current V1=V2, so
I1R1 = I2R2.
We also have I=I1+I2, so the currents I1 and I2 are given by,
because the
current does not go around the loop. The dipole
moment formula only works for current loops.
Instead, this is a current divider.
The current V1=V2, so
I1R1 = I2R2.
We also have I=I1+I2, so the currents I1 and I2 are given by,