


Next: About this document ...
PHY294H - Lecture21
The Hall effect
The Hall effect is a very important effect
in solid state physics, particularly in
semiconductor physics. It enables
us to determine, amongst many other things,
whether the dominant carriers are electrons
or holes. It works by applying
perpendicular electric and magnetic
fields to a material
which has a finite resistance. The electric field
produces a current flow in the direction of the
electric field, that is V=IR. The
magnetic field initially leads to a bending of the
charges which carry the current. However the bending of the
current leads to a charge build up
on the edges of the sample. This
in turn leads to a voltage perpendicular
to the direction of applied electric field and
also perpendicular to the applied magnetic field.
This is called the Hall voltage.
Eventually, the
Hall field is sufficient to balance the
magnetic force on the current, so that,
We thus find,
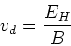 |
(2) |
Note that the polarity of the hall voltage
has opposite signs for hole carriers
and electron carriers.
The force between two current carrying wires
A DC current produces a magnetic field. This
was observed by Oersted in 1819 and by Ampere
in 1820. Ampere did a series of experiments to
deduce the magnetic field near a long straight
wire carrying a current I. He did this by
studying the force between two current carrying
wires. Consider two long straight wires which
are parallel to each other and which carrying
currents I1 and I2. Let us take the length
of the wires to be L and their separation to
be d. Ampere's experiments involved measuring the
force between the two long wires. He found
that the force is attractive for two wires
which carry current in the same direction,
while it is repulsive for wires carrying
currents in opposite directions. The
magnitude of the force was found to be,
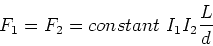 |
(3) |
The constant is defined to
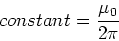 |
(4) |
This is a rather annoying but intrenched piece of notation, the permeability
is denoted 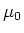 ,
which should not be confused with the
magnetic moment
,
which should not be confused with the
magnetic moment 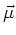 .
.
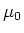 sets the scale
of forces and magnetic fields in magneto-statics in the
same way that
sets the scale
of forces and magnetic fields in magneto-statics in the
same way that
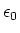 (or k) sets the scale of
forces and fields in electrostatics.
(or k) sets the scale of
forces and fields in electrostatics.
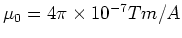 .
.
Now we want to deduce the magnitude and
direction of the
magnetic fields which are produced by the
wires. Since a DC current produces a magnetic
field, we may consider one of the wires to
produce a magnetic field and the other wire
to be influenced by it, that is,
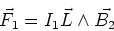 |
(5) |
In a similar way,
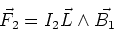 |
(6) |
By Newton's third law
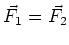 .
Comparing Eq. (3) and (5) it is evident that
the magnitude of the magnetic field due to
wire 1 is,
.
Comparing Eq. (3) and (5) it is evident that
the magnitude of the magnetic field due to
wire 1 is,
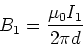 |
(7) |
Similarly
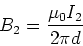 |
(8) |
Of course these magnetic fields are present even
if an isolated wire carries a current, I, so we
have the relation,
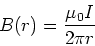 |
(9) |
which describes the magnetic field as a function of
distance from the wire. The direction of the magnetic field must
be perpendicular to the current and to the force between the
wires. This indicates that the magnetic field circulates
around the wire. The circulation of the magnetic field
is given by the right hand rule, again.
Ampere realised that his result for the
magnetic field near a wire may be written in the
form of a path integral.
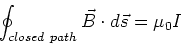 |
(10) |
Here 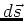 is a small vector along the direction of
the path. For example for a circle the unit vector is in tangent
to the circle. In this case, we have,
is a small vector along the direction of
the path. For example for a circle the unit vector is in tangent
to the circle. In this case, we have,
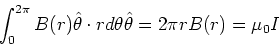 |
(11) |
Solving for B(r) yields equation (9).
Eq. (10) is Ampere's law and is one of two
tools that we will use to find the
magnetic field produced by currents. In this
form Ampere's law is correct only for DC,
time independent currents. Later in the
course we will add an additional term which
enables us to use this equation even
when there are time dependent fields.



Next: About this document ...
Phil Duxbury
2002-10-12