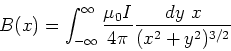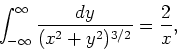Next: About this document ...
PHY294H - Lecture 22
Ampere's law and Gauss' law
Last lecture we followed Ampere's orginal
argument that the magnetic field near
a long straight wire behaves as,
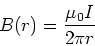 |
(1) |
The direction of the magnetic field is
given by the right hand rule.
A more general form of this relation is,
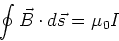 |
(2) |
I is the current which is enclosed
within the closed path.
This law enables us to choose the path of
integration. If we can choose paths on which the
magnetic field has simple behavior, then we can
deduce the magnetic field in a very simple manner.
This is similar to using Gauss' law in electrostatics.
Note that there is also a Gauss' law for magnetic
problems, so that the magnetic flux, 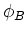 ,
through
a surface, S, is given by,
,
through
a surface, S, is given by,
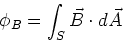 |
(3) |
which has the same form as the electric flux.
However since there are no free magnetic charges,
there is never any net enclosed magnetic charge
inside a closed surface.
Example 30.1
Finding the magnetic field inside
a current carrying wire. Consider a wire
which has circular cross-section of radius R, and
which carries current I which is uniformly
distributed throughout the wire cross-section.
Ampere's law is,
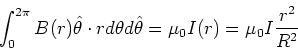 |
(4) |
From this we find,
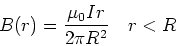 |
(5) |
For r>R, we have the usual relation
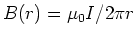 .
.
Example - The solenoid
Take a loop which is a rectangle of length l and width b. If the
solenoid is tightly packed, the magnetic field outside is zero. The
magnetic fields at each end of the rectangular path
should be the same, so on going
around the loop, their contributions cancel. The remaining piece
is the side which passes through the center of the solenoid. We
thus have,
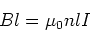 |
(6) |
where n is the number of turns per unit length. We thus have
the simple relation.
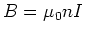
The thin toroid
We consider a solenoid which is formed into a
circle, where the diameter of the solenoid is
much smaller than the radius of the torus. We define
a path through the center of the torus. On this path
we expect the magnetic field to have the same magnitude,
therefore,
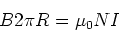 |
(7) |
So we have,
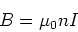 |
(8) |
as for the solenoid.
The Biot-Savart law
Ampere's law is great if we can find paths
on which the magnetic field is constant or at least
has a simple form.
However this is not always possible. Consider for
example a circular current loop. What magnetic field
does it produce? To do calculations of this
type, we need a new tool. The Biot-Savart law
gives us this tool. The Biot-Savart law is
a lot like the expression we used to
calculate the electric field due to
continuous charge distributions. In electrostatics,
the electric field produced by a small
element of charge dQ is given by,
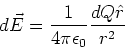 |
(9) |
The Biot-Savart law gives the magnetic field
produced by a small element of current.
The small element of current is usually
written as 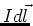 ,
that is a constant
current I flowing in a small length
of wire
,
that is a constant
current I flowing in a small length
of wire 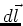 .
The magnetic field
given by this small element of current is,
.
The magnetic field
given by this small element of current is,
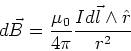 |
(10) |
The magnetic field is then found by
integration, ie.
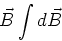 |
(11) |
Example - An infinite wire
Our first example is to find the magnetic
field due to an infinite wire. Consider
an infinite straight wire lying on the
y-axis. We seek the magnetic field
at a position x on the x-axis (i.e. at y=0).
Consider a small element of current,
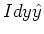 centered at position -y on the y-axis. The
distance from this element of current
to position x on the x-axis is,
centered at position -y on the y-axis. The
distance from this element of current
to position x on the x-axis is,
The magnitude of the cross product
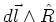 is
given by,
is
given by,
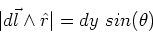 |
(13) |
where 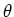 is the angle between the vectors
is the angle between the vectors 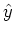 and
and 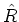 .
The direction of this cross product
is perpendicular to both
.
The direction of this cross product
is perpendicular to both 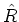 and
and 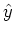 and
so is in the
z-direction for all values of y. That
is, the only finite component of B is in the z-direction.
Using the Biot-Savart law, we find the magnitude of
the z-component of B to be,
and
so is in the
z-direction for all values of y. That
is, the only finite component of B is in the z-direction.
Using the Biot-Savart law, we find the magnitude of
the z-component of B to be,
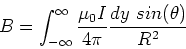 |
(14) |
From the geometry of the problem, we have,
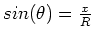 ,
so we find,
,
so we find,
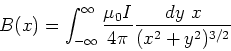 |
(15) |
Now we use the result,
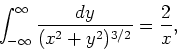 |
(16) |
so the final result is
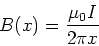 |
(17) |
Now note that the calculation above is the same
for any choice of the x-axis, which means that
our result is the same as that found by Ampere.



Next: About this document ...
Phil Duxbury
2002-10-12
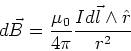
![]() centered at position -y on the y-axis. The
distance from this element of current
to position x on the x-axis is,
centered at position -y on the y-axis. The
distance from this element of current
to position x on the x-axis is,