


Next: About this document ...
PHY294H - Lecture 25
Recommended reading: FGT 852-3
Recommended problems: 31.45,31.46
Rotating loops - Electric Generators and motors
We will now show that if we
rotate a loop at constant
angular speed in a uniform and constant
magnetic field, then we generate an
oscillatory emf. In an electric generator,
we rotate a loop through a magnetic
field using a chemical or nuclear
energy source. This produces the oscillatory
emf we use in our society. An electric
motor works in reverse. If we apply
an oscillatory emf to a current loop in a
magnetic field, it rotates at constant
angular speed. Recall that in the
case of a DC current source, we had to
switch the current direction every 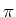 rotation in order to keep the loop moving
in the same direction. However in
the case of an AC motor, the AC source
switches polatity automatically every
rotation in order to keep the loop moving
in the same direction. However in
the case of an AC motor, the AC source
switches polatity automatically every
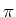 rotation, so the direction of rotation
of the loop is maintained.
rotation, so the direction of rotation
of the loop is maintained.
Let us consider the situation in which
a coil with N turns and area Ais rotated about its central axis at constant
angular speed 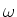 .
The angle between
the magnetic moment of the loop and the
applied magnetic field is
.
The angle between
the magnetic moment of the loop and the
applied magnetic field is 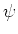 .
This
angle increases as
.
This
angle increases as
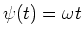 due
to the constant angular speed of the coil.
The rate of change of the magnetic flux is
due
to the constant angular speed of the coil.
The rate of change of the magnetic flux is
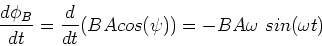 |
(1) |
The induced emf is given by Faraday's which gives,
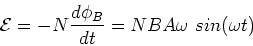 |
(2) |
The potential energy is given by,
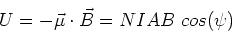 |
(3) |
The torque is given by,
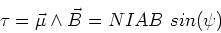 |
(4) |
The mechanical power that must be supplied to
rotate the coil is,
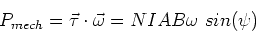 |
(5) |
This must be equal to the electrical power delivered to the
load, this is given by,
 |
(6) |
The average power dissipated is
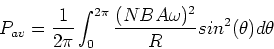 |
(7) |
Using the result that,
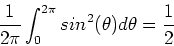 |
(8) |
we have,
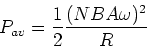 |
(9) |
which is the average power delivered by our generator. This
is the number you see quoted on your lightbulb.



Next: About this document ...
Phil Duxbury
2002-10-17
![]() rotation in order to keep the loop moving
in the same direction. However in
the case of an AC motor, the AC source
switches polatity automatically every
rotation in order to keep the loop moving
in the same direction. However in
the case of an AC motor, the AC source
switches polatity automatically every
![]() rotation, so the direction of rotation
of the loop is maintained.
rotation, so the direction of rotation
of the loop is maintained.
![]() .
The angle between
the magnetic moment of the loop and the
applied magnetic field is
.
The angle between
the magnetic moment of the loop and the
applied magnetic field is ![]() .
This
angle increases as
.
This
angle increases as
![]() due
to the constant angular speed of the coil.
The rate of change of the magnetic flux is
due
to the constant angular speed of the coil.
The rate of change of the magnetic flux is