| (1) |
A time varying magnetic field
So far we have considered cases where the
applied magnetic field is constant and uniform
while the area through which the field
passes has been altered by mechanical means. Consider
now a region of space in which the
magnetic field is increasing as
B(t) = B0 + B1t.
we want to find the electric field that this
changing magnetic field induces. We use Faraday's law
to find,
| (1) |
| (2) |
Recall that if we have a time varying electric
field
E(t) = E0 + E1 t, then we carry out an analogous
calculation using the Maxwell displacement term to find,
| (3) |
| (4) |
Example - A rotating rod
Consider a conducting rod at angle ![]() to the x-axis.
The rod is rotated at constant angular speed w so the
angle increases as
to the x-axis.
The rod is rotated at constant angular speed w so the
angle increases as
![]() .
Close
the loop by making a circular pie segment with the x-axis
and the rod as its bounding radii. The rate of change
of flux is given by,
.
Close
the loop by making a circular pie segment with the x-axis
and the rod as its bounding radii. The rate of change
of flux is given by,
| (5) |
| (6) |
| (7) |
Example: Moving crossbar
Consider a rectangular loop where one
of the sides is a freely movable crossbar,
while the other sides are fixed. The loop
lies in constant B field which
is parallel with the loop normal. If the
wire making up the loop and the crossbar
has resistance
![]() ,
the
crossbar has length L=10cm, the
crossbar is moving at speed 5m/sand the magnetic field has magnitude
B = 1T, find: a) The force required to maintain the
speed of the crossbar; b) The power
dissipated in the rectangular
loop.
,
the
crossbar has length L=10cm, the
crossbar is moving at speed 5m/sand the magnetic field has magnitude
B = 1T, find: a) The force required to maintain the
speed of the crossbar; b) The power
dissipated in the rectangular
loop.
The induced emf is given by,
| (8) |
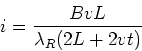 |
(9) |
| F = i L B | (10) |
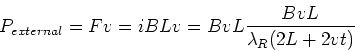 |
(11) |
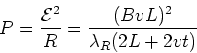 |
(12) |
Example - Eddy currents
A piece of metal dropped through a magnetic field
also has induced electric fields and induced
currents. These currents are called eddy
currents and can be quite large. They
lead to resistive losses, ie.
![]() losses.
It is evident that the larger the resistance
the smaller the losses, for fixed induced emf.
One strategy for reducing eddy current losses is then
to laminate or in other ways increase
the resistance of a piece of metal.
losses.
It is evident that the larger the resistance
the smaller the losses, for fixed induced emf.
One strategy for reducing eddy current losses is then
to laminate or in other ways increase
the resistance of a piece of metal.
A bar magnet and a loop
If we move a bar magnet toward a conducting loop,
there is an induced current in the loop.
The induced current produces
a magnetic field that looks like an induced
bar magnet. The magnitude of the induced bar magnet
is dependent on the resistance of the
loop, the size of the real bar magnet
and the speed at which we move the real
bar magnet toward the loop.
An important special case - A superconductor
Superconductors are a special case where
the induced currents occur even in a
constant magnetic field. That is,
even constant fields induce currents
which oppose the applied field. This
effect leads to a variety of new applications
such as magnetic levitation.