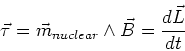Next: About this document ...
PHY294H - Lecture 29
Nuclear magnetic resonance(NMR)
Nuclear magnetic resonance works by controlling
the magnetic moment of nuclei. Usually a nucleus
which has a net spin of 1/2 is used as this
is the case where the theoretical analysis
is well understood. The magnetic moment of
a proton or a neutron is about 2000 times
smaller than the magnetic moment of an electron.
However if a large magnetic field is applied
to a nucleus, the magnetic field produces
a significant splitting of the up and down
energy levels of the nuclear spin,
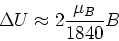 |
(1) |
where 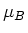 is the Bohr magneton. Now an
oscillatory field is applied and resonance occurs
when,
is the Bohr magneton. Now an
oscillatory field is applied and resonance occurs
when,
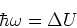 |
(2) |
By measuring the resonant absorption, it is
possible to figure out how many nuclear magnetic
moments are present in the material. A closer
loop at which is happening at the atomic level
is evident upon considering a quantum mechanical
magnetic dipole in the applied field B. The
torque on the dipole is,
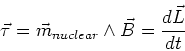 |
(3) |
The fundamental postulate of quantum mechanics is the
the magnitude of L is fixed. This means that the
quantum magnetic moment cannot align with the applied
field. Instead it precesses around the direction of the magnetic field.
The frequency of this precession is called the Larmour frequency.
resonance occurs when the Larmour frequency is equal
to the frequency of the applied oscillatory magnetic field.
In medical applications NMR is called MRI (medical
resonance imaging) and the Hydrogen nucleus is
used as the target nucleus (different nuclei
have different resonant frequencies). MRI
measures the local amount of absorption and
so gives an estimate of the number of H nuclei
in the part of the human body to which it is
applied. Since fat has a high concentration
of H nuclei, while bone has a low concentration,
there is good contrast between fat and bone.
MRI is complementary to X-rays which scatter
most strongly from high mass nuclei. MRI
can be extended to provide a probe of the
velocity of the protons and also the local
environment of the protons. This is call
functional MRI.
Self-Inductance (L)
We now look at the way in which
magnetic field effects are used
in circuit applications. In
circuit applications, we want
to related the emf across a
circuit element to the current
through the element. Consider
placing a solenoid in a circuit.
We know that the magnetic field
in the solenoid is given by,
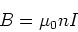 |
(4) |
where I is the current through the
solenoid. The flux through the
solenoid is
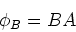 |
(5) |
where A is the cross-sectional area
of the solenoid. The emf across the
solenoid is then,
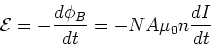 |
(6) |
where N = nl is the number of loops in
the solenoid. It is thus evident that the
induced emf across the solenoid is proportional
to the rate of change of the current and that
the induced emf opposes the change in current.
This is the circuit version of Faraday's law.
In circuits, we write,
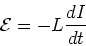 |
(7) |
where L is the inductance. This
is true for any configuration of current
carrying wires, not just for the solenoid.
The only thing that depends on the
wire geometry is the inductance. For a solenoid,
we find,
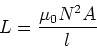 |
(8) |
The self-inductance thus
tells us how the current and
voltage are related in a current
carrying wire configuration.
Mutual inductance
Since the magnetic fields of one
current carring wire configuraiton
may influence a second
wire, it is natural to consider
the way in which two wire configurations
are coupled through their magnetic
fields. This coupling is
described by the mutual inductance.
We write,
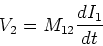 |
(9) |
Consider for example a small solenoid, of area A2
and N2 turns and of length l2 inside
a solenoid (with N1 turns, length l2 and
area A2) which carries current I1, so that
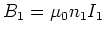 .
The flux passing
through the small solenoid is
.
The flux passing
through the small solenoid is
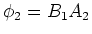 .
If we change the current I1, we change the
flux through the loop so that,
.
If we change the current I1, we change the
flux through the loop so that,
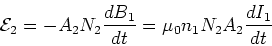 |
(10) |
The mutual inductance is then,
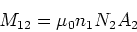 |
(11) |
Doing a similar calculation for the
inner solenoid gives
Energy stored in inductors
The rate at which work is done in an
inductor is given by,
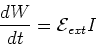 |
(13) |
We have shown that the voltage across
an inductor is -LdI/dt, so we have,
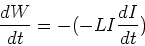 |
(14) |
The energy stored in an inductor is thus,
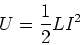 |
(15) |
This energy is stored in the magnetic field
of the inductor, for example in a solenoid we
have,
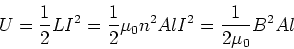 |
(16) |
The energy density in the magnetic field is then,
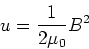 |
(17) |



Next: About this document ...
Phil Duxbury
2002-10-23