


Next: About this document ...
PHY294H - Lecture 3
Recommended work related to Lecture 3:
Read: FGT pp 618-629
Do problems: 23.9, 23.10, 23.16, 23.17
We want to undertand and control electric fields. First
we need to know how to make a uniform electric field.
Uniformly charged sheet
Consider a uniformly charged sheet, with charge
density
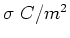 .
To find the electric field near such a sheet,
we can use the result we found for a thin ring of charge, namely,
.
To find the electric field near such a sheet,
we can use the result we found for a thin ring of charge, namely,
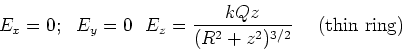 |
(1) |
The electric field for an infinite sheet is found by
integrating this expression from R=0 to 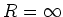
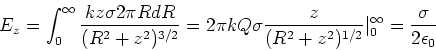 |
(2) |
Thus a uniformly charged sheet produces a uniform electric field. If
two plates of equal and opposite uniform charge are placed parallel to
each other, the electric field is simply a sum of the electric
fields due to the individual sheets (superposition holds). This
demonstrates that two parallel uniformly charged sheets (of opposite
charge) have electric field
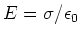 between
them and zero electric field outside. This is the standard method
for generating a uniform electric field for
use in cathode ray tubes, accelerators etc.
between
them and zero electric field outside. This is the standard method
for generating a uniform electric field for
use in cathode ray tubes, accelerators etc.
Charge moving in a uniform field
If a charge moves through a region of space where the
electric field is uniform, it undergoes an acceleration
given by,
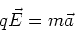 |
(3) |
Example
Consider a charge q moves with initial speed v in the
x-direction. This charge enters a region of uniform
electric field, 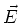 ,
which is directed along the
positive y direction. If the charge experiences this
electric field for d=1cm, find the velocity of the
charge after it has left the region of space in which
the electric field exists.
,
which is directed along the
positive y direction. If the charge experiences this
electric field for d=1cm, find the velocity of the
charge after it has left the region of space in which
the electric field exists.
Solution
The velocity in the x-direction is unaltered, so vx=v.
The velocity in the y direction is given by,
The amount of time the charge is in the field is
t=d/vx=d/v.
The acceleration in the
y-direction is
ay = q |E|/m and
vy(0) = 0. We thus have,
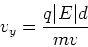 |
(5) |
Dipole in a uniform electric field
Torque
A dipole in a uniform field experiences a torque. To calculate
the torque, we start with the definition of torque,
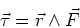 |
(6) |
The point of rotation is the center of the dipole and the
force is due to the uniform electric field
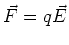 where E is the electric field.
In a uniform field, the force on the negative charge of the
dipole is equal and opposite to the force on the positive charge
of the dipole. We have
where E is the electric field.
In a uniform field, the force on the negative charge of the
dipole is equal and opposite to the force on the positive charge
of the dipole. We have
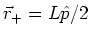 ,
,
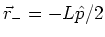 and
and
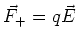 ,
,
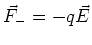 .
We then have
.
We then have
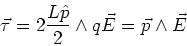 |
(7) |
Note that the magnitude of the torque is given by,
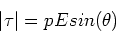 |
(8) |
where 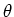 is the angle between the direction of the
electric field and the direction of the dipole. From this
expression we see that if the dipole is parallel or antiparallel to the
applied field, there is no torque. The torque is a maximum
when the dipole is perpendicular to the field.
is the angle between the direction of the
electric field and the direction of the dipole. From this
expression we see that if the dipole is parallel or antiparallel to the
applied field, there is no torque. The torque is a maximum
when the dipole is perpendicular to the field.
Potential energy
Using the principles of mechanics we calculate the
energy of the dipole as a function of its
orientation with respect to the applied field. Actually
we shall calculate the change in potential energy
required to rotate the dipole through an angle 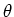 with respect to the field. We have,
with respect to the field. We have,
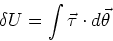 |
(9) |
Both
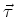 and
and
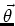 are perpendicular to the
plane of rotation of the dipole so we have,
are perpendicular to the
plane of rotation of the dipole so we have,
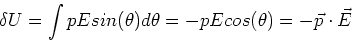 |
(10) |
The potential energy is lowest when the dipole and the electric field
are aligned. The potential energy is highest when the
dipole is antiparallel with the field, even though the torque is
zero in that state.



Next: About this document ...
Phil Duxbury
2002-09-24
![]() .
To find the electric field near such a sheet,
we can use the result we found for a thin ring of charge, namely,
.
To find the electric field near such a sheet,
we can use the result we found for a thin ring of charge, namely,
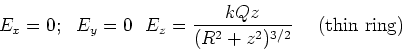
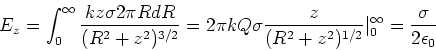
![]() ,
which is directed along the
positive y direction. If the charge experiences this
electric field for d=1cm, find the velocity of the
charge after it has left the region of space in which
the electric field exists.
,
which is directed along the
positive y direction. If the charge experiences this
electric field for d=1cm, find the velocity of the
charge after it has left the region of space in which
the electric field exists.
![]() with respect to the field. We have,
with respect to the field. We have,