


Next: About this document ...
PHY294H - Lecture 30
RL circuits, DC source
Kirchhoff's loop law for
a circuit containing a DC voltage
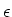 ,
a resistor R and
an inductor L is,
,
a resistor R and
an inductor L is,
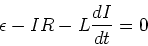 |
(1) |
The solution to this equation is,
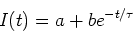 |
(2) |
where
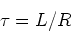 |
(3) |
The constants a and bdepend on the initial conditions.
Initial current is zero
In this case, we imagine that a
switch is in the circuit and that
the switch is open for t<0.
We thus have I(0) = 0. This implies that
Since there is no current at time t=0,
the voltage across the resistor is zero
at t=0. Therefor the entire voltage
is dropped across the inductor. We thus
have,
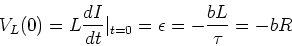 |
(5) |
From this equation we find,
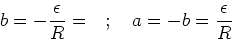 |
(6) |
The current in the circuit is then,
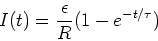 |
(7) |
At long times(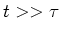 ), the inductance plays no role
in this DC circuit.
), the inductance plays no role
in this DC circuit.
Initial current is I0, no applied voltage
In this case we have,
We also have
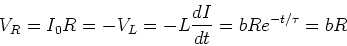 |
(9) |
We then have,
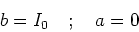 |
(10) |
so that,
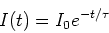 |
(11) |
An LC circuit - an oscillator
A circuit with an inductor and a capacitor
acts as an oscillator. There is no
dissipation in this circuit, provided
the capacitor and the inductor are ideal.
We shall consider a case in which the
capacitor has charge Q0 at t=0 and that
at this time there is no current
flowing in the circuit. The capacitor at
time t=0 stores energy Q02/C, while
the inductor stores no energy at t=0.
At time t=0, we then have,
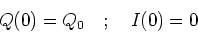 |
(12) |
As time goes on, energy is exhanged between
the capacitor and the inductor. This
is very similar to the exchange
between kinetic and potential
energy in a spring-mass system
or in a pendulum.
Kirchhoff's loop law for the LC ciruit
is,
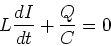 |
(13) |
Since I=dQ/dt, this equation is equivalent to,
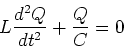 |
(14) |
This is the equation for simple harmonic motion and
has the general solution,
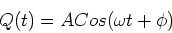 |
(15) |
where A and 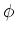 are constants which
we may choose to satisfy the initial conditions.
In our example, the initial conditions are,
Q(0) = Q0 and I(0) = 0, which are
satisfied by,
are constants which
we may choose to satisfy the initial conditions.
In our example, the initial conditions are,
Q(0) = Q0 and I(0) = 0, which are
satisfied by,
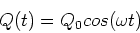 |
(16) |
LRC circuit
We are just adding
a resistor to the problem we
solved above. Kirchhoff's loop law gives
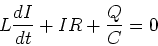 |
(17) |
Using I=dQ/dt we find,
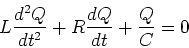 |
(18) |
The general solution to this equation is,
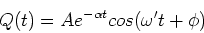 |
(19) |
where A and 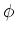 are constants which
are chosen to fit the initial conditions.
are constants which
are chosen to fit the initial conditions.
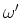 and
and 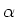 are found by
subsituting Eq. (19) into equation (18)
and ensuring that Eq. (19) is a solution
for all time.
To carry out this calculations, we need to take
derivatives of the charge with the respect
to time. The first derivative is,
are found by
subsituting Eq. (19) into equation (18)
and ensuring that Eq. (19) is a solution
for all time.
To carry out this calculations, we need to take
derivatives of the charge with the respect
to time. The first derivative is,
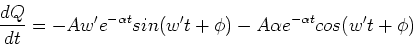 |
(20) |
and
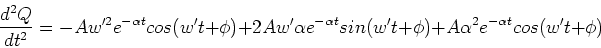 |
(21) |



Next: About this document ...
Phil Duxbury
2002-10-24
![]() ,
a resistor R and
an inductor L is,
,
a resistor R and
an inductor L is,