


Next: About this document ...
PHY294H - Lecture 32
Transformers - Using Mutual inductance
Transformers are the first example of a circuit in which
we apply an alternating current (AC) source. When we
consider the mutual inductance of two concentric solenoids,
we found,
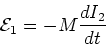 |
(1) |
The mutual inductance we found was,
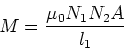 |
(2) |
In a transformer, we couple two coils using
a high permeability magnetic core (e.g. Fe or Permalloy).
If this coupling is perfect, we get the same mutual inductance as that of
concentric solenoids. The self-inductance of
a solenoid is,
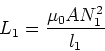 |
(3) |
Now we consider applying an oscillatory current (AC)
source to one of the coils of a transformer. The
applied current source applies an oscillatory
voltage source,
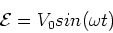 |
(4) |
Let us assume that this produces a voltage
across the first solenoid which
is given by,
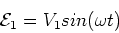 |
(5) |
The current through the first solenoid is then
found from,
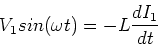 |
(6) |
which implies,
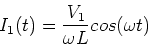 |
(7) |
The voltage across the second solenoid is then,
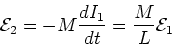 |
(8) |
Using Eq. () and (), we have,
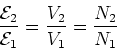 |
(9) |
If N2>N1 this is called a step up transformer, while
if N2<N1 it is called a step down transformer.
In an ideal transformer no power is lost, so we
must have,
which implies
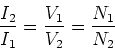 |
(11) |
A step up transformer has a step up in voltage, but
a step down in current. A step down transformer steps
down the voltage but steps up the current. Now consider
the power lost in transmitting power down a transmission line
which has resistance R. The loss is given by,
If we seek to deliver a power Pdel. We do not know the
load resistance, but we do know that the power delivered using the
transmission line is
Pdel = VI. Using this to
eliminate I in the above, we find
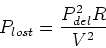 |
(13) |
This means that the power lost is less if R is smaller and
if V is large. That is, high voltage transmission lines
are most efficient.
AC circuits
We already have treated some of the behaviors
to be found in circuits containing inductors
capacitors and resistors. We are going to
analyse the ciruits again, but now with an AC
voltage source. It is still true that ideal inductors
and capacitors only store energy while
resistors dissipate energy. The time constants for
 and
and 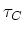 are still important, however
they only apply to transients in the circuit response.
We shall consider the steady state response of
circuits with AC sources. The natural frequency
are still important, however
they only apply to transients in the circuit response.
We shall consider the steady state response of
circuits with AC sources. The natural frequency
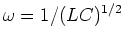 ,
as we shall see, is the same as
the resonant frequency of an LRC circuit with
an AC source. To understand the behavior of
AC circuits, we will introduce the concept of the reactance
of a circuit element and also the idea of the phase of the
current through the circuit and the phase relation
between the current though a circuit element
and the voltage across that circuit element.
,
as we shall see, is the same as
the resonant frequency of an LRC circuit with
an AC source. To understand the behavior of
AC circuits, we will introduce the concept of the reactance
of a circuit element and also the idea of the phase of the
current through the circuit and the phase relation
between the current though a circuit element
and the voltage across that circuit element.
A resistor in series with an AC source
This is the simplest case as usual, but it is useful to
define the notation using this simple case.
We have an AC voltage source given by,
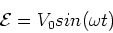 |
(14) |
As usual Kirchhoff's loop law yields,
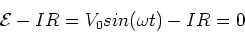 |
(15) |
Solving for the current we find,
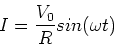 |
(16) |
It is evident that this is the same as for a DC circuit.
However for later reference, note that the phase of the
current is the same as the phase as the voltage across the
resistor.
A capacitor in series with an AC source
Kirchhoff's loop law now gives,
 .
Solving for the charge on the capacitor as
a function of time, we thus find,
.
Solving for the charge on the capacitor as
a function of time, we thus find,
 .
To find the current, we use,
.
To find the current, we use,
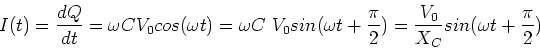 |
(17) |
From this expression we see that the current ``leads'' the voltage in
a capacitor. This is natural as the capacitor has to charge
up before it has a voltage so the current flow is ahead of the voltage.
In the last expression we have defined the capacitive reactance,
 .
This acts like an effective resistance due to
a capacitor. Note that if the frequency goes to zero,
a capacitor has infinite reactance, while as frequency
goes to infinite it has very small reactance.
.
This acts like an effective resistance due to
a capacitor. Note that if the frequency goes to zero,
a capacitor has infinite reactance, while as frequency
goes to infinite it has very small reactance.
An inductor in series with an AC source
Kirchhoff's loop law now gives,
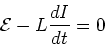 |
(18) |
Solving for the charge on the capacitor as
a function of time, we thus find,
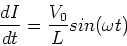 |
(19) |
To find the current, we integrate to find,
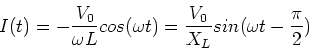 |
(20) |
From this expression we see that the current ``lags'' the voltage in
an inductor. This is natural as the inductor resists
a change in current (which would lead to a change in
magnetic field in the coils of the inductor). We have
defined the inductive reactance
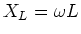 .
The
inductive reactance is larger at high frequency as
there the rate of change of current is high and the
inductor resists a change in current. At low frequencies the
inductive reactance goes to zero as there
the rate of change of current is slow and hence
there is little induced emf, from Faraday's law.
.
The
inductive reactance is larger at high frequency as
there the rate of change of current is high and the
inductor resists a change in current. At low frequencies the
inductive reactance goes to zero as there
the rate of change of current is slow and hence
there is little induced emf, from Faraday's law.



Next: About this document ...
Phil Duxbury
2002-10-30
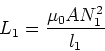
![]() and
and ![]() are still important, however
they only apply to transients in the circuit response.
We shall consider the steady state response of
circuits with AC sources. The natural frequency
are still important, however
they only apply to transients in the circuit response.
We shall consider the steady state response of
circuits with AC sources. The natural frequency
![]() ,
as we shall see, is the same as
the resonant frequency of an LRC circuit with
an AC source. To understand the behavior of
AC circuits, we will introduce the concept of the reactance
of a circuit element and also the idea of the phase of the
current through the circuit and the phase relation
between the current though a circuit element
and the voltage across that circuit element.
,
as we shall see, is the same as
the resonant frequency of an LRC circuit with
an AC source. To understand the behavior of
AC circuits, we will introduce the concept of the reactance
of a circuit element and also the idea of the phase of the
current through the circuit and the phase relation
between the current though a circuit element
and the voltage across that circuit element.
![]() .
Solving for the charge on the capacitor as
a function of time, we thus find,
.
Solving for the charge on the capacitor as
a function of time, we thus find,
![]() .
To find the current, we use,
.
To find the current, we use,