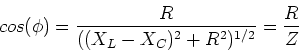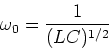Next: About this document ...
PHY294H - Lecture 33
Steady state response - Driven LRC circuit
Consider an AC source
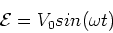 |
(1) |
applied to a series LRC combination. We shall
consider the case in which this source
has been applied to the circuit for
long enough time for all transients
to have dissappeared. In this limit,
the current in the circuit has the same
frequency as the AC source, however
it may have a different phase, as was the
case for the simple inductor and capacitor
examples. Kirchhoff's law implies,
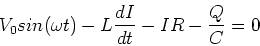 |
(2) |
or,
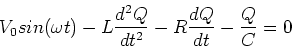 |
(3) |
We shall solve for the charge as a function of time and
from it find the current using I = dQ/dt. The
steady state solution to the equation above is,
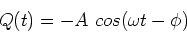 |
(4) |
In this problem, the constants A and 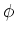 are found
by subsituting this assumption back into
the equation above. Note that this is
different than the transition LRC case where A and
are found
by subsituting this assumption back into
the equation above. Note that this is
different than the transition LRC case where A and 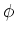 were determined by the initial conditions. Here
we are looking at the steady state of a driven
system and this enables us to find A and
were determined by the initial conditions. Here
we are looking at the steady state of a driven
system and this enables us to find A and 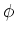 in general. We shall find the current,
in general. We shall find the current,
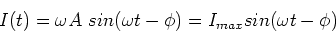 |
(5) |
Finding A and 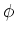
We shall need two trigonometric identities,
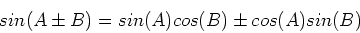 |
(6) |
and
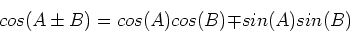 |
(7) |
We then write,
![\begin{displaymath}Q = -Acos(\omega t-\phi) = -A[cos(\omega t)cos(\phi)
+ sin(\omega t)sin(\phi)]
\end{displaymath}](img9.gif) |
(8) |
![\begin{displaymath}{dQ\over dt} = A\omega\ sin(\omega t - \phi)
= A\omega[sin(\omega t)cos(\phi) - cos(\omega t)sin(\phi)]
\end{displaymath}](img10.gif) |
(9) |
![\begin{displaymath}{d^2Q\over dt^2} = A\omega^2\ cos(\omega t-\phi) = A\omega^2
[cos(\omega t)cos(\phi) + sin(\omega t)sin(\phi)]
\end{displaymath}](img11.gif) |
(10) |
We now use these expressions in Eq. (3) and set the
coefficient of the
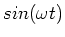 term to zero,
which gives,
term to zero,
which gives,
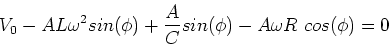 |
(11) |
Setting the coefficent of the
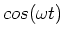 term to zero yields,
term to zero yields,
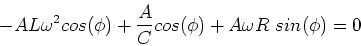 |
(12) |
The latter equation yields,
![\begin{displaymath}tan(\phi) = {1\over R}[\omega L - {1\over \omega C}] = {X_L - X_C\over R}
\end{displaymath}](img16.gif) |
(13) |
This also implies that
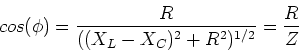 |
(14) |
where Z is the impedance, defined by,
|
Z = (R2+(XL - XC)2)1/2.
|
(15) |
We also have,
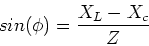 |
(16) |
Using these relations in Eq. (11) we have,
![\begin{displaymath}V_0 - A\omega[{X_L-X_C \over Z}(X_L - X_C ) + R{R\over Z}] = 0
\end{displaymath}](img19.gif) |
(17) |
Solving for A we find,
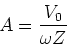 |
(18) |
The current in the circuit is then given by,
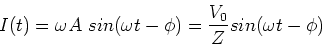 |
(19) |
The voltage across the resistor is
given by,
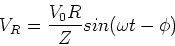 |
(20) |
The voltage across the capacitor is,
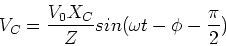 |
(21) |
The voltage across the inductor is,
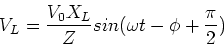 |
(22) |
Resonance
If we plot the phase angle and the impedance
as a function of frequency, it is evident
that there is a special frequency at which
the impedance is small. This special
frequency occurs when the capacitive and
inductive reactances cancel,
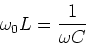 |
(23) |
This special frequency is just the
natural frequency of the LC combination,
ie.
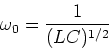 |
(24) |
At resonance, the phase angle is zero so the
current is in phase with the source.



Next: About this document ...
Phil Duxbury
2002-10-30
![]()