Optics, Electricity and Magnetism were considered to be unrelated subjects prior to 1820. In 1820 Ampere and Oersted demonstrated that electric current influences magnets. It was not until 1864 that optics and other electromagnetic waves were unified and their relation to electricity and magnetism was made clear, by James Clerk Maxwell. For unifying all of these subjects, the equations we have been working with are collectively called Maxwell's equations. Maxwell generalised Ampere's equation by adding the displacement current term to it. The resulting equation is called the generalised Ampere's law. Maxwell then showed that the generalised Ampere's law in combination with Faraday's law, and using Gauss' law, leads to the possibility of propagating electric and magnetic fields. These fields propagate away from a source and have wavelike form, so they are called electromagnetic waves.
The first observation to make is that any accelerating charge produces a time varying magnetic field. In addition, a time varying magnetic field produces a time varying electric field. These time varying electric and magnetic fields propagate outward from the source and they are the electromagnetic waves which we plan to study. For example a charge moving in a circular accelerator emits radiation. Similarly, an AC current in a wire emits radiation. The frequency of the radiation is designed by choosing the source frequency and also the geometry of the wire in which the charges are flowing.
The simplest receiving antenna is a loop. When an
em wave moves through the loop, it induces an emf
in the loop which is amplified and detected.
The bigger the loop and the greater the number of turns
the better the receiver.
Another antenna is a ferrite bar receiver, which is
used in practically all radios. We also need
a tuning capacitor 10-365pF.
Television FM 90-120MHz. VHF 54-216MHz.
AM band. 150kHz and below - military.
150Hz-540Hz
navigation beacons.
540kHz-1700KHz - AM radio.
1700-1800kHz not much.
1800kHz-2Mz - Ham radio (160m).
2-2.3MHz - Marine communications, distress at 2.182MHz.
Some math that we need
We define ![]() to be a vector field, like the
magnetic or the electric field. The divergence of
to be a vector field, like the
magnetic or the electric field. The divergence of
![]() is given by,
is given by,
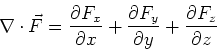 |
(1) |
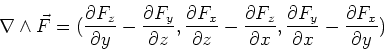 |
(2) |
Divergence theorem
The integral of the divergence of ![]() over a volume, V, is equal to the
integral of the component of the
function through the surface, S, which encloses this
volume. This is mathematically stated as,
over a volume, V, is equal to the
integral of the component of the
function through the surface, S, which encloses this
volume. This is mathematically stated as,
| (3) |
Stokes theorem
The line integral of a vector function
around a closed loop is equal to the
curl of the function through the
any surface, S, which is enclosed by the
line integral.
| (4) |