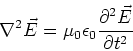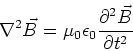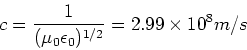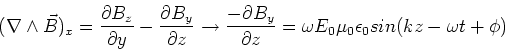Next: About this document ...
PHY294H - Lecture35
Divergence theorem
The integral of the divergence of 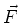 over a volume, V, is equal to the
integral of the component of the
function through the surface, S, which encloses this
volume. This is mathematically stated as,
over a volume, V, is equal to the
integral of the component of the
function through the surface, S, which encloses this
volume. This is mathematically stated as,
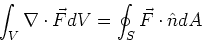 |
(1) |
Stokes theorem
The line integral of a vector function
around a closed loop is equal to the
curl of the function through
any surface, S, which is connected
to the closed loop.
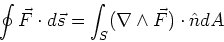 |
(2) |
Relation between current and current density
The relation we need is,
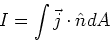 |
(3) |
Gauss' law for electric field
The Electric flux, 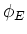 ,
through a closed surface,
S is equal to the net charge, q, enclosed within
that surface.
,
through a closed surface,
S is equal to the net charge, q, enclosed within
that surface.
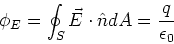 |
(4) |
Differential form,
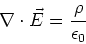 |
(5) |
Gauss's law for magnetic field
The Magnetic flux, 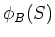 ,
through a closed surface,
S is equal to zero.
,
through a closed surface,
S is equal to zero.
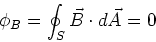 |
(6) |
Differential form
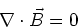 |
(7) |
Generalized Ampere's law
The path integral of the magnetic field
around any closed loop, is equal to the current enclosed
by the loop plus the displacement current enclosed by the loop.
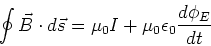 |
(8) |
Differential form
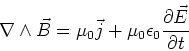 |
(9) |
Faraday's law
The emf induced in a closed loop, is equal
to the rate of change of the magnetic flux, 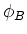 ,
through the closed loop,
,
through the closed loop,
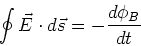 |
(10) |
Differential form
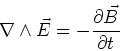 |
(11) |
The equations for EM waves in free space
In free space, there are no wires so the term
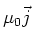 is not needed. We want to combine Eq. (9) and (11). If we
take a time derivative of Eq.(9) and then use Eq. (11), we find,
is not needed. We want to combine Eq. (9) and (11). If we
take a time derivative of Eq.(9) and then use Eq. (11), we find,
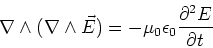 |
(12) |
If we take a time derivative of (11) then use Eq. (9) we find,
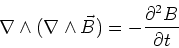 |
(13) |
An identity that is easy to prove (e.g. using Mathematica!) is,
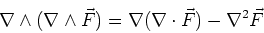 |
(14) |
Now note that in free space
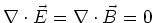 ,
Using these expressions in Eqs. (12) and (13), we find,
,
Using these expressions in Eqs. (12) and (13), we find,
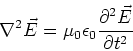 |
(15) |
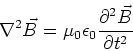 |
(16) |
These are both wave equations, which just means that they
have solutions which are of the form,
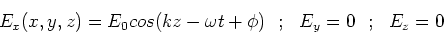 |
(17) |
This is an EM wave which travels in the
z-directionand whose electric field oscillates in the x direction.
Similar solutions exist for waves travelling in the
x-direction and in the
y-direction.
Most of the physics can be deduced from this
one component of the field.
If we subsitute this expression into Eq.(15), we
find,
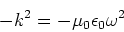 |
(18) |
or, using
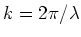 ,
,
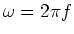
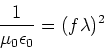 |
(19) |
This demonstrates that the velocity of the
wave is,
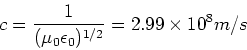 |
(20) |
This discovery is considered one of the most important
of the 19th century and provides the unification
of optics, electricity and magnetism.
Since we have
taken the Ey=Ez=0, we have,
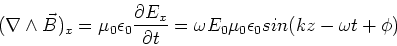 |
(21) |
We also have,
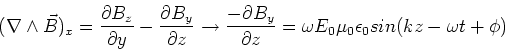 |
(22) |
If we integrate this expression with respect to z, we find,
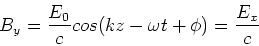 |
(23) |
This expression shows that the magnetic field is
oscillating in phase with the electric field. The electric
field oscillates in the x direction, the magnetic field
oscillates in the y-direction and the wave
travels in the z-direction.



Next: About this document ...
Phil Duxbury
2002-11-08
![]() over a volume, V, is equal to the
integral of the component of the
function through the surface, S, which encloses this
volume. This is mathematically stated as,
over a volume, V, is equal to the
integral of the component of the
function through the surface, S, which encloses this
volume. This is mathematically stated as,
![]() ,
through a closed surface,
S is equal to the net charge, q, enclosed within
that surface.
,
through a closed surface,
S is equal to the net charge, q, enclosed within
that surface.
![]() ,
through a closed surface,
S is equal to zero.
,
through a closed surface,
S is equal to zero.
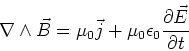
![]() ,
through the closed loop,
,
through the closed loop,
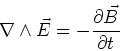
![]() is not needed. We want to combine Eq. (9) and (11). If we
take a time derivative of Eq.(9) and then use Eq. (11), we find,
is not needed. We want to combine Eq. (9) and (11). If we
take a time derivative of Eq.(9) and then use Eq. (11), we find,