| (1) |
Two views of light
Light as a wave - From Maxwell's equations
Linearly polarized (with the electric field in the x-direciton)
EM waves moving through free space
are described by,
| (1) |
| (2) |
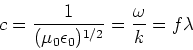 |
(3) |
| (4) |
| (5) |
Note that if light travels in matter, its speed changes to,
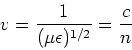 |
(6) |
| (7) |
Light as a particle - from quantum mechanics and relativity
Two key equations that we need are from modern physics. Planck showed that
light comes in bundles of energy called photons, where the energy of a
photon is related to its frequency, f, by,
| (8) |
| (9) |
| (10) |
Note that many of the experiments with light may be
interpretted using either the wave theory
or particle (quantum) theory.
This was the origin of many controversies concerning the
theory of light in the 19th and early 20th centuries.
Of course the full quantum theory of light
contains the wave picture in the classical limit,
which is a delight to be anticipated in higher
level physics courses.
Important properties of light
From the structure of EM waves, we will now understand the
energy density, the energy flux, the momentum and the
polarization properties of these waves.
Energy density u
First let's look
at the energy density, u, of an EM wave. This is easy to write
down as we already know the energy density of electric and
magnetic fields, so we have,
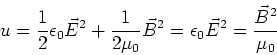 |
(11) |
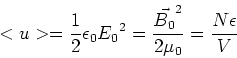 |
(12) |
Energy flux (power) and Poynting vector, ![]()
Water waves and waves on strings carry energy. EM waves do too.
Oscillating electric and magnetic fields can lead to motion
of charges which is the way in which EM waves transfer
their energy to matter. The amount of energy
which is available per unit time per unit area is called
the energy flux. We write,
| dU = A c u dt | (13) |
| (14) |
| (15) |
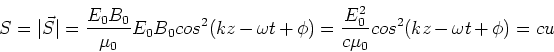 |
(16) |
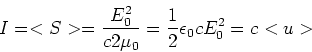 |
(17) |
Momentum density
Water waves and waves on strings have momentum. Their momentum
is due to the motion of the media in which they travel.
EM waves also have momentum. This is harder to see classically,
however from the quantum viewpoint it is evident. De Broglie's
relation is
![]() which relates the momentum to the
wavelength of a wave and to Planck's constant h. Nevertheless
it is possible to deduce the momentum of an EM wave from
classical arguments. This is evident upon placing
a positive charge in the path of the EM wave. When the electric
field is in the positive x direction, it accelerates
the charge in that direction. This charge moves in the
presence of the magnetic field which is in the
y-direction,
The magnetic force on this moving charge is in the z direction,
that is, in the direction of motion of the wave. The wave
thus pushes the charge in the direction of motion of the wave.
Momentum is thus transferred from the EM wave to the charged
particle. It is possible to derive the relation we need
from this argument.
which relates the momentum to the
wavelength of a wave and to Planck's constant h. Nevertheless
it is possible to deduce the momentum of an EM wave from
classical arguments. This is evident upon placing
a positive charge in the path of the EM wave. When the electric
field is in the positive x direction, it accelerates
the charge in that direction. This charge moves in the
presence of the magnetic field which is in the
y-direction,
The magnetic force on this moving charge is in the z direction,
that is, in the direction of motion of the wave. The wave
thus pushes the charge in the direction of motion of the wave.
Momentum is thus transferred from the EM wave to the charged
particle. It is possible to derive the relation we need
from this argument.
However, the most natural way to find the relation between the energy
density of the wave and the momentum density of the wave is
to use the particulate nature of the light. Using
![]() ,
the momentum density is given by,
,
the momentum density is given by,
| (18) |
Radiation pressure
Photons may be reflected or absorbed. Since photons carry
momentum, these events lead to pressure at the macroscopic
scale. This pressure is called radiation pressure and
is the pressure which stops the sun from collapsing.
Consider a flat surface. Photons which hit the flat
surface may reflect or absorb. Let's assume normal incidence,
that is their velocity is normal to the surface.
If they reflect elastically from the surface,
a momentum of
![]() is transferred to the
surface, while if they are absorbed by the surface,
a momentum of
is transferred to the
surface, while if they are absorbed by the surface,
a momentum of
![]() is transferred to the surface. In general there is
partial relection and partial absorption, in which case we have,
is transferred to the surface. In general there is
partial relection and partial absorption, in which case we have,
![]() ,
with
,
with ![]() for absorption and
for absorption and ![]() for reflection, for normal incidence. Clearly reflection is more
effective at transferring momentum. The pressure is the
force per unit area p = F/A. The force is the
rate of change of momentum which is the change in
momentum due to one photon hitting the surface times
the number hitting the surface per unit time, that is
for reflection, for normal incidence. Clearly reflection is more
effective at transferring momentum. The pressure is the
force per unit area p = F/A. The force is the
rate of change of momentum which is the change in
momentum due to one photon hitting the surface times
the number hitting the surface per unit time, that is
| (19) |
| (20) |
Dipole radiation
The intensity is the average power per unit area and for
a light wave is given by,
| (21) |
| (22) |
Geometrical optics - reflection and refraction
In many cases, the behavior of light can be understood
by using rays to trace the way in which a beam of
light reflects from surfaces and the
way in which a beam of light refracts when passing
through a surface. Mirrors, lenses, telescopes
and microscopes can all be understood using the
simple principles of geometrical optics. There are
two basic laws of geometrical optics which describe
the way in which light rays behaves at a surface,
Reflection law
The angle of incidence is equal to the angle of reflection,
![]() .
.
Refraction law (Snell's law)
| (23) |
Note: Angles are measured with respect to the
normal to the surface.