Polarisation
Linear polarisation - Electric field oscillates in one direction.
Unpolarised - Random mixture of polarisation in all
directions. If unpolarised light is passed through a polariser
then 1/2 of the intensity passes through and the outgoing
light is linearly polarised.
Circularly polarised - Electric field vector rotates as the wave
propagates. If we add two waves which are in phase, but which are linearly
polarised in the x and y-directions respectively we get a wave which
is linearly polarised at 45o. If we add the same two waves but
now with a phase difference ![]() between them, we can have
elliptically polarised light. The special case of
between them, we can have
elliptically polarised light. The special case of
![]() is circularly polarised light and righthanded. The
case
is circularly polarised light and righthanded. The
case
![]() is lefthanded. The case
is lefthanded. The case
![]() is
again linearly polarised.
is
again linearly polarised.
Polaroid - Aligned long molecules of
polyvinyl alcohol(PVA) impregnated with Iodine. The Iodine acts as
an electron donor and gives the PVA molecules electronic
conductivity.
Use of polarisation in wireless communication
Linearly polarised light has an electric field which
oscillates in one direction.
Long distance communications are sent with horizontal polarisation.
This is better as vertically polarised light is more susceptible
to attenuation by treetops. In contrast local broadcasts
are sent with vertical polarisation. This is due to the
fact that vertical receivers are more convenient
on cars and rooftops. The fact that local and long
distance communications have opposite polarisation
directions also helps reduce interference.
Polarisation by scattering
To understand scattering it is convenient to think in terms of charges which are accelerated by the electric field in the EM wave. Accelerated charges emit radiation. They emit the radiation predominantly perpendicular to their direction of acceleration.
We consider scattering of an unpolarised beam
of light. Scattering can be visualised as the
instigation of oscillation of the charges
from which the light scatters. This oscillation leads
to a dipole radiation field which we observe as
the scattered light. If we observe this scattering
along the direction of the incident light, then
the oscillations of the charges in the scatterer
are always perpendicular to our line of sight.
In contrast if we observe the scattering at 90o to the
direction of propagation, we will observe light that is vertically
polarised. The horizontal component is eliminated.
the scattered radiaion is preferentially polarised perpendicular
to the plane of the scattering.
Reflection off a surface is an important example. Unpolarised light
which is scattered off a surface is preferently polarised
perpendicular to the plane of the scattering. The
most extreme case is where the transmitted and
reflected rays are at 90o. This is the Brewter angle ![]() The light obeys Snell's law which states that
The light obeys Snell's law which states that
![]() .
In addition for maximum
polarisation, we need the scattered and transmitted rays
to be at 90o. This implies that
.
In addition for maximum
polarisation, we need the scattered and transmitted rays
to be at 90o. This implies that
![]() .
The special angle at which this occurs is called the
Brewster angle
.
The special angle at which this occurs is called the
Brewster angle ![]() where we have,
where we have,
| (1) |
| (2) |
Dispersion - wavelength dependence of refractive index
Dispersion: n depends on frequency. At high frequency (blue)
n is larger.
To discuss dispersion effects, we first
have to expand our discussion of light.
Our discussion so far has been focused on
light of one wavelength. This light is called monochromatic
light. White light has a mixture of wavelengths (colors)
and is called polychromatic or polydisperse.
The key new feature we shall use is that
the refractive index of many optical materials depends
on the wavelength of the incident light. This
is called dispersion and is the reason that light
produces colors when it is passed through a
prism. For example the refractive index of light
varies from n=1.528 in the blue to n=1.51 in the
red. This small variation leads to easily observed
splitting of the colors of the spectrum. Examples
are refraction through a prism and the physical
origin of rainbows.
Rayleigh scattering - the wavelength dependence of scattering
Rayleigh Scattering: Scattering intensity is larger
at higher freqencies (shorter wavelength).
![]() .
.
If there was no atmosphere, the sky would
be black except if we looked
straight at the sun. The fact that the sky is not black
is due to scattering of light from
air molecules and particles in the
atmosphere. The color that we see is due to the
fact that light scattering is stronger at short wavelengths,
because it is easier for the electrons in
small particles to be excited by short wavelength
light. This means that we see a predominantly blue
color in the sky.
Atomic origin of dispersion
The simplest model is to consider a
mass spring system as a model for the electron/nucleus
system. This system has a resonant frequency
![]() .
When an electric field of frequency
.
When an electric field of frequency ![]() is incident on
this system, resonance occurs when
is incident on
this system, resonance occurs when
![]() .
Light in this regime is at much lower frequency than the
resonant frequency, so we have,
.
Light in this regime is at much lower frequency than the
resonant frequency, so we have,
![]() .
The
diplacement of the electron is approximated by,
.
The
diplacement of the electron is approximated by,
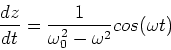 |
(3) |
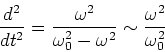 |
(4) |
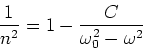 |
(5) |
Properties of light
As we have seen, the classical theory of optics allows us to vary a variety of properties of light
- Wavelength
- Polarisation
- Relative phase
- Amplitude
These properties all have quantum interpretations.
The light over which we have most control is laser
light, where we control the phase relation of photons
as well as the other properties above. However
the photon has spin 1 and we would like to know
how that is related to the properties above.
The correspondence is that circularly polarised
light has a net angular momentum. The right
circularly polarised case corresponds to
spin -1, while the left polarized light
corresponds to spin 1. Spin zero corresponds to
in phase x and y components of the electric field.