Spherical refracting surfaces
Last lecture, we saw that parallel
rays incident upon a spherical mirror
have a common focal point, provided that the
angle of reflection is sufficiently small
(
![]() ). For concave mirrors
the focal length is positive, for
convex mirrors the focal length is negative.
Parallel light rays incident upon
a spherical refracting surface also have
a common focal point. The relation between
the focal length and the radius of the
spherical surface is,
). For concave mirrors
the focal length is positive, for
convex mirrors the focal length is negative.
Parallel light rays incident upon
a spherical refracting surface also have
a common focal point. The relation between
the focal length and the radius of the
spherical surface is,
| (1) |
Ray diagrams can again be used to show that an image is formed by a spherical refracting surface. The principal rays in this case are:
1. A parallel incoming ray is refracted through the focal point.
2. A ray which passes through the center of curvature is not refracted.
The relations between the image and source are now,
| (2) |
| (3) |
The sign conventions for refracting surfaces are:
- The image distance is positive when
it is on the opposite side to the source.
- The radius of curvature is taken
to be positive when the center of curvature
is on the opposite side to the approaching
rays of light.
- The magnification is negative for
inverted images.
Now we consider a more complex case, where we have two refracting surfaces. In this case we first treat the first refracting surface and find its image. Then we use that image as the source for the second refracting surface. This procedure sometimes leads to a new situation, namely cases where the image from the first refracting surface is on the real image side of the second refracting surface. This case can be treated with the formula above provided we introduce the sign convention:
- Object distances are negative if the object is on the real image side of the refracting surface.
With this definition and the rules
for constructing rays given above,
we can carry out calculations for a sequence
of refracting surfaces. This enables us
to derive the thin lens formulae given below.
Thin lenses
The thin lens laws are applications of the equations
for a refracting surface. A thin lens
is two refracting surfaces which
are close to each other.
If we place such a lens in air, the
effect of the first refractive
surface is to produce an image whose
position is
found from,
| (4) |
| (5) |
| (6) |
| (7) |
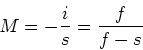 |
(8) |
Sign convention for R1 and R2
Again the rule is that the radii R1 or R2 are
negative if the approaching rays of light are on the same side
as the center of curvature.
Principle rays for thin lenses
- 1. An incoming ray parallel to the central axis of the lens is refracted to (or from) the focal point.
- 2. A ray that passes through the focal point is refracted to an outgoing ray which is parallel to the central axis(converging lens).
- 3. A ray passes through the center of the lens undeflected (this is a thin lens approximation).