| (1) |
How the human eye works
The human eye is an extraordinary optical instrument. Light is focused on the retina which consists of about 108 photoreceptors which come in two types, rods and cones. These photoreceptors are attached to 106 axons of ganglion cells. The ganglion cells make up the optic nerve which transmits impulses to the brain. The photoreceptors detect individual photons. All of the ganglions in the optic nerve have a slow steady firing rate, even in the dark. A diffuse light does not affect this rate. However an more intense directed beam of light induces a rapid increase in the firing rate of the ganglions attached to the photoreceptrs attached to the rods and cones where this light is focused (http://users.rcn.com/jkimball.ma.ultranet/BiologyPages/V/VisualProcessing.html).
Light is focused on parts of the retina by the lens.
The lens is long and thin when we look at distant objects.
It is short and fat when we look at close objects, e.g.
when we read. In the relaxed state, the lens is long and
thin. If the resting state of the lens is not thin enough,
light from distant objects are is focused before the retina.
This is a condition called near-sightedness and is the
most frequent vision problem in the very young. In contrast
if the lens cannot be made convergent enough to focus
the light from close objects on the retina, then
the person is far-sighted. This is the most frequent
vision problem of adults, who then require reading glasses.
Angular size
In our discussion of mirrors, refracting surfaces
and lenses, we have defined mangification to be
M=-i/s = hi/hs. This definition is not the
most useful one when considering optical instruments
such as microscopes and telescopes. In these instruments
the key measure of magnification is the angular size
of an object or image.
The angle subtended by an
object, or by an image is,
| (1) |
Maximum angular size achievable with the naked eye
The way in which we can increase the angular magnification of
an object, using only the naked eye,
is simply to move our eyes closer to it. This
is limited by the ability of the lens in our eye
to focus the light from near objects onto the retina. The
closest objects which can be brought into focus by
adults is about 25cm, so the angular extent
that the naked eye can achieve is
| (2) |
Angular magnification - Simple magnifier
The simple magnifier (magnifying glass) is a convergent
lens which can assist the eye by allowing the eye
to move even closer to the object of interest.
Converging lenses produce a magnified, virtual, image
when the object is placed inside the focal length of the
lens. If the object is placed at the focal point of the
lens, then the image is at infinity, and the magnification
is
M = -i/f = hi/hs. The angular extent of the image produced by the
magnifier, ![]() ,
is
,
is
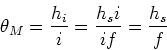 |
(3) |
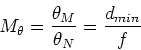 |
(4) |
Compound microscope
Much larger angular magnifications can be achieved using the compound microscope. This instrument is attributed to Hans and Zacharias Jansen in 1590 though they only achieved 9x magnification. In the 1700's however early compound microscopes could magnify up to about 250 times, which opened up direct observation of the world of microbiology. This was first achieved by Anton van Leeuwenhoek in 1676 who made the first direct observations of bacteria. Modern optical microscopes can achieve up to 2000x magnification, but they are ultimately limited by diffraction effects due to the wavelength of light.
The compound microscope consists of two converging lenses. The
object is placed in front of an objective lens. The object is
placed just outside the focal length of the objective lens and the
object is lighted from behind. The objective, which has
focal length f1, produces a
real inverted and magnified image.
A second lens (the
eyepiece) is placed so that the image from the
objective is just inside the focal length, f2, of the eyepiece.
This results in a magnified virtual image, as for the simple
magnifier treated above. The distance between the
objective and the eyepiece is L. The image distance
of the objective lens is,
i1 = L - f2. The
magnification due to the objective is then,
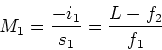 |
(5) |
| (6) |
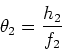 |
(7) |
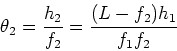 |
(8) |
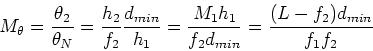 |
(9) |
Telescopes
The refracting telescope, probably first developed in Holland
but Galileo built one of his own in 1609, consists of two converging lenses.
As for the microscope, the first lens is the objective
and the second is the eyepiece.
The first lens takes the stars (sources at infinity)
and forms an image, which is placed at the focal length
of the eyepiece, which acts as a simple magnifier.
The stars we wish to observe have an angular size
![]() .
The image we observe in the eyepiece
has angular extent
.
The image we observe in the eyepiece
has angular extent ![]() .
The focal lengths
of the objective and eyepiece are f1 and f2
respectively. We have,
.
The focal lengths
of the objective and eyepiece are f1 and f2
respectively. We have,
| (10) |
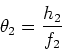 |
(11) |
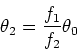 |
(12) |
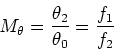 |
(13) |
The majority of modern telescopes are reflecting telescopes
which work on the same principle except the objective
is a large concave mirror. Newton is credited with developing the first
reflecting telescope (1668).
Aberrations
There are many errors that can occur in telescopes and in microscopes. Monochromatic aberrations occur for light of one wavelength and include errors in machining the curvature of the lens (like the Hubble space telescope) and errors in focusing even if the lens was perfectly spherical (remember the small angle approximation we used?).
Chromatic aberrations occur in lenses due to the fact that the refractive index is different for different wavelengths. One of the advantages of the reflecting telescope is that mirrors do not suffer from chromatic aberration, though of course the eyepiece lens still does. Chromatic aberrations can be corrected using a second, diverging, lens that negates the chromatic aberrations of the converging lens system. Parabolic mirros can be designed to spherical aberrations. The final limiting factor is again diffraction effects due to the fact that light has a finite wavelength, as we shall see in a week or so.