


Next: About this document ...
PHY294H - Lecture 43
The ray analysis we used in geometrical optics
did not achnowledge the wave nature of light.
The light traveled in straight lines, except
for reflection and refraction. The wave
nature of light is evident in two types
of phenomena, interference and diffraction.
These effects are most evident when the wavelength
of light is close to the size of the
object or hole that we are interested in.
Even when the size of an object is
considerably larger than the wavelength of light
we can see interference and diffraction effects
by use a screen which is a long way from the
scattering event or events.
Phase differences and interference
Waves from two different sources interfere.
You have probably observed this with water waves at the beach
and in ripples on ripple tanks.
In order for interference to occur, in a
well defined way, the light from
the two sources needs to have a well
defined relative phase and it is simplest if they
have the same polarisation. In all interference
experiments we need to compare the phase
of the waves arriving from two or more
sources. If the waves are in phase they
add constructively, while if they are
out of phase they cancel each other (
they add destructively). Often we shall
calculate the phase difference,
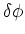 ,
between the waves coming from two sources.
In that case we have the following conditions:
,
between the waves coming from two sources.
In that case we have the following conditions:
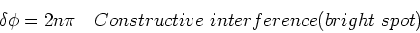 |
(1) |
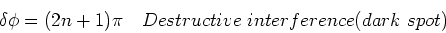 |
(2) |
where n is an integer.
There are many ways to change the phase difference
between the two waves, including differences in
path-length, differences in refractive index
experienced by the two rays, differences in
phases of the two sources.
Young's double slit experiment
Young's double slit experiment consists of a coherent light
source incident upon two slits. The light coming out of the
slits is like the light coming from two pencil-like
sources of light, which are in phase. The light
arriving at different locations on a screen have
different path lengths. The distance from a point
on the screen to one of the slits is l1, while the
distance from a point on the screen to the other slit
is l2. Now we need to relate distance to phase.
The relation is that one wavelength corresponds to
a phase of 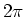 .
The phase difference between the
two light waves arriving from the two sources is
then,
.
The phase difference between the
two light waves arriving from the two sources is
then,
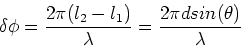 |
(3) |
[Aside: The equation
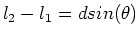 is a small angle
approximation. The complete relation goes as follows: Consider the
three lengths: l1 from the first(upper) slit to a position P on the
screen; l from a point midpoint between the slits to point P;
l2 from the second(lower) slit to the screen. The line l makes
an angle
is a small angle
approximation. The complete relation goes as follows: Consider the
three lengths: l1 from the first(upper) slit to a position P on the
screen; l from a point midpoint between the slits to point P;
l2 from the second(lower) slit to the screen. The line l makes
an angle 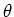 with the horizontal. Consider the triangle
formed by l, l1 and the vertical distance d/2 between the
center point between the slits and the upper slit. The angle
between l and the vertical in this triangle is
with the horizontal. Consider the triangle
formed by l, l1 and the vertical distance d/2 between the
center point between the slits and the upper slit. The angle
between l and the vertical in this triangle is 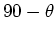 .
Using the cosine rule on this triangle yields,
.
Using the cosine rule on this triangle yields,
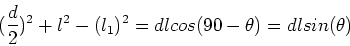 |
(4) |
Similarly, the lower triangle yields,
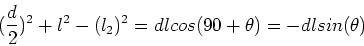 |
(5) |
Subtracting the second equation from the first gives
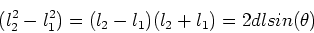 |
(6) |
From this it is seen that the pathlength difference is
given by,
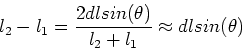 |
(7) |
where the last expression involves the approximation
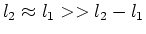 .]
.]
The angles at which maxima are located are found from
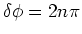 ,
which gives,
,
which gives,
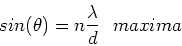 |
(8) |
and for minima,
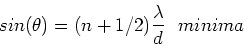 |
(9) |
where n is an integer.
The intensity pattern
The pathlength argument above
only gives the location of the maxima and minima.
Now we want to find the intensity pattern
that we see on the screen. To find the intensity
at a point on the screen, we calculate,
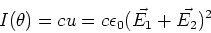 |
(10) |
We shall take the waves to have to have the same polarization
and only differ by a phase given by Eq. (3). We thus write,
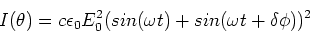 |
(11) |
Use the trigonometric identity,
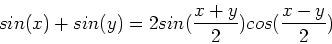 |
(12) |
So that,
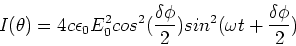 |
(13) |
This may be written as,
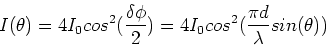 |
(14) |
where I0 is the intensity due to a single source.
Interference due to films and air gaps
When light is incident on any interface, some
reflection occurs, even if the material is
transparent (e.g. reflections off glass).
The light which reflects off the top surface
may interfere with the light which
reflects off the bottom surface of a
thin film. This is the origin of color in
thin soap films, oil films and in narrow air
gaps. These films look colored due to the
fact that the different colors have different
wavelengths, leading to different locations for the
maxima and minima of the interference patterns. We shall
illustrate the phenomena for monochromatic light,
as we did for Young's experiment.
Interference due to an air gap
Consider two flat plates of glass which make
an air wedge. If we illuminate this wedge
with monochromatic light, an interference
pattern is produced in which the
light reflected from the
top surface of the air wedge interferes
the light reflected from the bottom surface
of the air wedge. If the air wedge has
a small angle 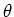 ,
then the
size of the air gap is given by,
,
then the
size of the air gap is given by,
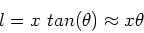 |
(15) |
The light which reflects from the bottom surface of the air wedge
travels an additional distance 2l(for near normal
incidence), which leads to
a phase difference
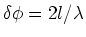 .
To
determine the conditions constructive and destructive
interference, we need to know one other important
fact:
.
To
determine the conditions constructive and destructive
interference, we need to know one other important
fact:
- When light reflects from a surface where n1>n2,
there is no phase change of the reflected light.
- When light reflects from a surface where n1<n2,
there is a phase change of 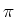 of the reflected light.
of the reflected light.
This is analogous to what happens with waves on
strings where the density of the string replaces the
refractive index. Given this information,
we find,
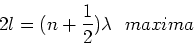 |
(16) |
and
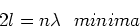 |
(17) |



Next: About this document ...
Phil Duxbury
2002-11-27
![]() ,
between the waves coming from two sources.
In that case we have the following conditions:
,
between the waves coming from two sources.
In that case we have the following conditions:
![]() .
The phase difference between the
two light waves arriving from the two sources is
then,
.
The phase difference between the
two light waves arriving from the two sources is
then,
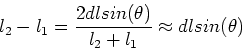
![]() ,
which gives,
,
which gives,
![]() ,
then the
size of the air gap is given by,
,
then the
size of the air gap is given by,
![]() of the reflected light.
of the reflected light.