Interference due to a thin oil film
When interference occurs due to a thin film with
refractive index n, we have to take into account the
fact that the wavelength of light is shorter inside
the thin film. [ Recall that the speed of light inside
a material with refractive index n is, vn = c/n.
The frequency however is the same, so we have,
![]() and
and
![]() .
Taking the
ratio of these equations yields
.
Taking the
ratio of these equations yields
![]() .
]
The number of wavelengths of light inside a thickness
2 l is then,
.
]
The number of wavelengths of light inside a thickness
2 l is then,
![]() .
Notice that the only
modification to our previous analysis
is that
.
Notice that the only
modification to our previous analysis
is that
![]() .
.
Interferometers
We have seen that the wave nature of light leads
to easily observed effects in a variety of situations,
but typically when there is a length scale which is
of order the wavelength of light or smaller. The typical
wavelength of light is ![]() ,
so light can be sensitive
to rather small lengths. This sensitivity is used as
a tool in interferometers.
,
so light can be sensitive
to rather small lengths. This sensitivity is used as
a tool in interferometers.
Michelson interferometer
Michelson invented the interferomenter near the end of the 19th century. It was used in the famous Michelson-Morley experiment which indicated the absence of an ``ether''.
The Michelson interferometer produces interference fringes by
splitting a beam of monochromatic light so that one beam
strikes a fixed mirror (this beam has pathlength l1)
and the other a movable mirror (this beam has pathlength l2. When the
reflected beams are brought back together, an interference
pattern results. As usual the condition for constructive
interference is
![]() .
Note that if the media
through which the beams travel is different for the two paths, then the
path lengths l2 and l1 must be modified. For example
if path l1 is through air and path l2 is through water,
then the length of path 2 must be multiplied by the
refractive index of water.
.
Note that if the media
through which the beams travel is different for the two paths, then the
path lengths l2 and l1 must be modified. For example
if path l1 is through air and path l2 is through water,
then the length of path 2 must be multiplied by the
refractive index of water.
Fabry-Perot interferometer
The Fabry-Perot interferometer uses multiple reflections
of the two beams to enhance the interference pattern.
This is achieved by using two parallel mirrors one of
which is a partially transmitting mirror.
Diffraction
Consider breaking up the single slit diffraction
process up into 2N+1 sources equally spaced
in a slit of width a. The spacing between
adjacent sources is a/2N, as we place
one source at each edge of the slit.
The electric field at a position on the screen
at angle to the center is then,
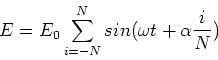 |
(1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Multiple slit interference pattern
The intensity of a multiple slit interference pattern,
where there are N slits separated by distance d is
given by,
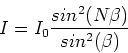 |
(8) |
| (9) |
| (10) |