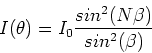 |
(1) |
Multiple slit grating
Light which travels through a set of N parallel slit, with
slits which are very narrow, leads to the intensity pattern,
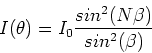 |
(1) |
| (2) |
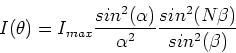 |
(3) |
| (4) |
x-ray diffraction, Von Laue (1912)
Crystal lattices have regular spacings, so if
light is reflected from them, the scattered light
looks like the light being emmitted from a
set of point sources. There are intensity maxima at
angles which are given by (for a geometry where the
incoming light is at angle ![]() to a crystal plane
and we measure the outgoing light at the same angle,
to a crystal plane
and we measure the outgoing light at the same angle,
| (5) |
Diffraction limits on resolution
To understand diffraction limits on resolution of microscopes
and telescopes, we first
need to understand the diffraction pattern due to a circular hole
of diameter D. The diffraction pattern due to such a hole
is a set of concentric light and dark rings. The first
maximum is at zero angle (of course) and the first minimum
is at an angle of
| (6) |
Resolution of the compound microscope
The object is placed at the focal length of the objective
lens. The separation of features that can be resolved
on the microscope slide is then(using
![]() ),
),
| (7) |
Resolution of the human eye A similar
calculation can be applied to the human eye, where we take
D = 2.5mm and
![]() .
.
Resolution of telescopes
The angular resulution of telescopes is simply ![]() ,
where D is the diameter of the primary lens or mirror.
Earth bound telescopes have less resolution than this
due to atmospheric turbulence. The Hubble space telescope has
resolution which is close to the diffraction limit.
Spy satellites have the
same problem as earth bound telescopes and the best resolution they
have, in observing objects on earth, is about 1m.
,
where D is the diameter of the primary lens or mirror.
Earth bound telescopes have less resolution than this
due to atmospheric turbulence. The Hubble space telescope has
resolution which is close to the diffraction limit.
Spy satellites have the
same problem as earth bound telescopes and the best resolution they
have, in observing objects on earth, is about 1m.
For both telescopes and microscopes the first lens or mirror that the incoming light is incident up is the most important for the diffraction limit on resolution. If the sources are not resolved by the first element in the optical system, then the other optical elements cannot help. In addition the angle of the intermediate image is amplified, making the diffraction effects of the later elements less important.