PHY294H - Lecture 8

If we move a charge q from a point a to a point b, then the charge in potential energy, U_ab, of the system is

$$\Delta U_{ab} = -\int_a^b \vec{F}\cdot\vec{ds}$$ (1)

- $\vec{F}$ is the electric force on charge q due to all of the other charges in the system

- $\vec{ds}$ is a small displacement along the path we choose to take from a to b.
If we define the electric potential to be the potential energy per unit charge, so that V=U/q, then the difference in electric potential is given by,

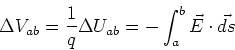$$\Delta V_{ab} = {1\over q}\Delta U_{ab} = -\int_a^b \vec{E}\cdot\vec{ds}$$ (2)

We define the potential energy and hence the potential of a charge at infinity to be zero.

With the definition of potential given in Eq. (2) and taking the potential at infinity to be zero, we can calculate the potential at each position from the electric field.

Electric potential due to a point charge

The electric field due to a point charge is

$$\vec{E} = {k Q \hat{r}\over r^2}$$ (3)

The electric potential due to a point charge is then,

$$V = -\int_{\infty}^r {k Q \hat{r}\over r^2}\cdot \vec{ds} = ... ... dr \hat{r} = -kQ \int_{\infty}^r {dr\over r^2} = {kQ\over r}$$ (4)

Uniform shell of charge

From the shell theorems we know that the electric field inside a uniform shell of charge is zero. In addition, if the electric field is zero the integral (2) gives no contribution so the electric potential is a constant. The electric potential of a uniform shell of charge is therefore a constant inside the shell of charge and like a point charge centered at the origin outside the shell of charge.

Conductors

Inside and on the surface of conductors, the electrical potential is a constant. This follows as the electric field is zero inside and parallel to the surface of conductors.

Parallel plates

If we consider two parallel plates with uniform charge density $\sigma$, then the electric field between the plates has magnitude $\sigma/\epsilon_0$. Since this is a constant, the electric potential difference between the plates is simply E d where d is the distance between the plates. The electric potential is defined as the potential to move a small positive charge between two positions. In this case we imagine moving a small positive charge from the negative plate to the positive plate. This requires work and hence the electrical potential is positive. The electric potential of the positively charged plate is thus higher than the electric potential of the negatively charged plate.