The Standard Model inclusive Higgs
cross section is known at LO, NLO
and NNLO.
The Higgs
tranverse momentum distribution has been calculated to to NNLO+NNLL.
The link
to the discussion of Higgs production in CHS can be found here.
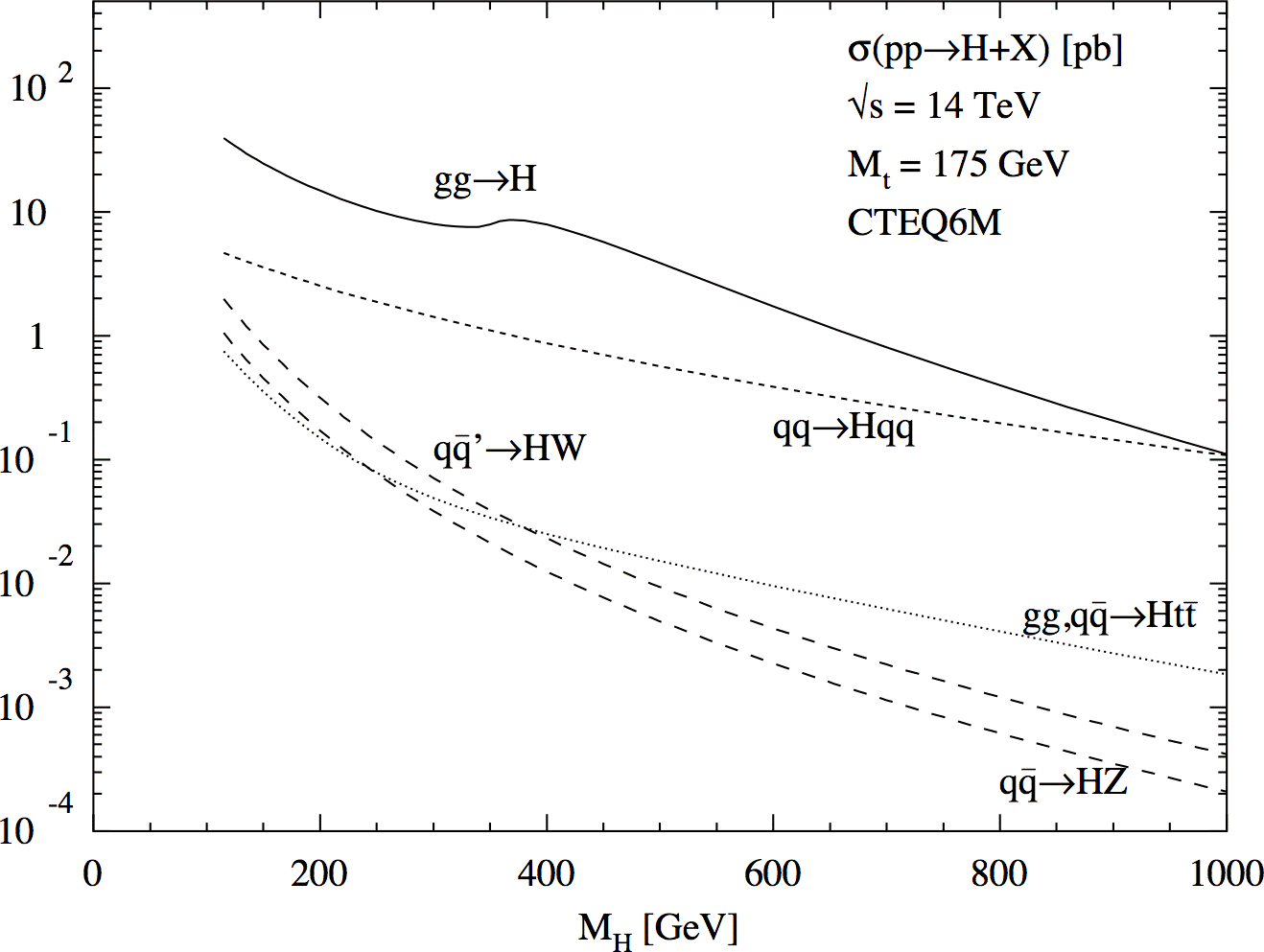
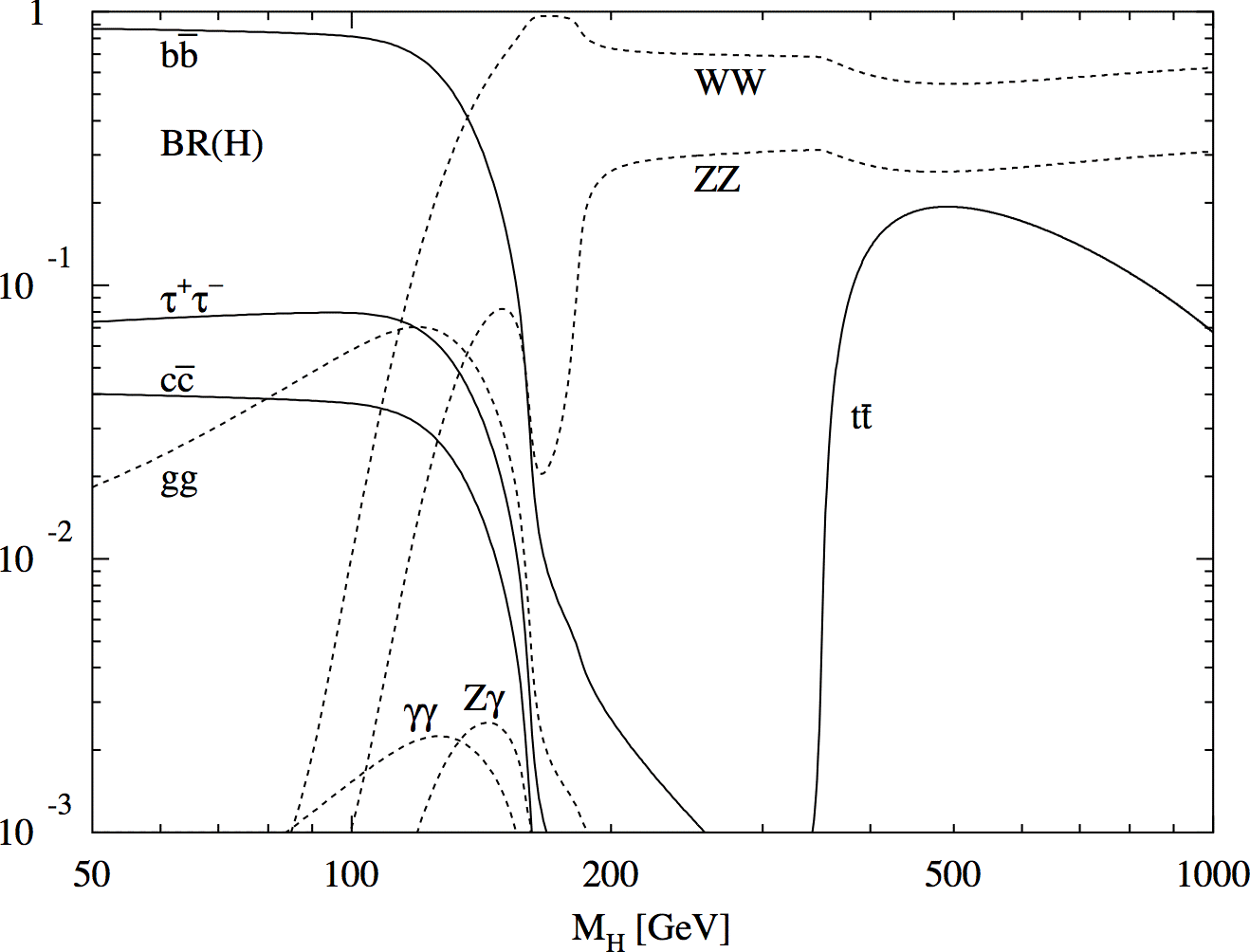
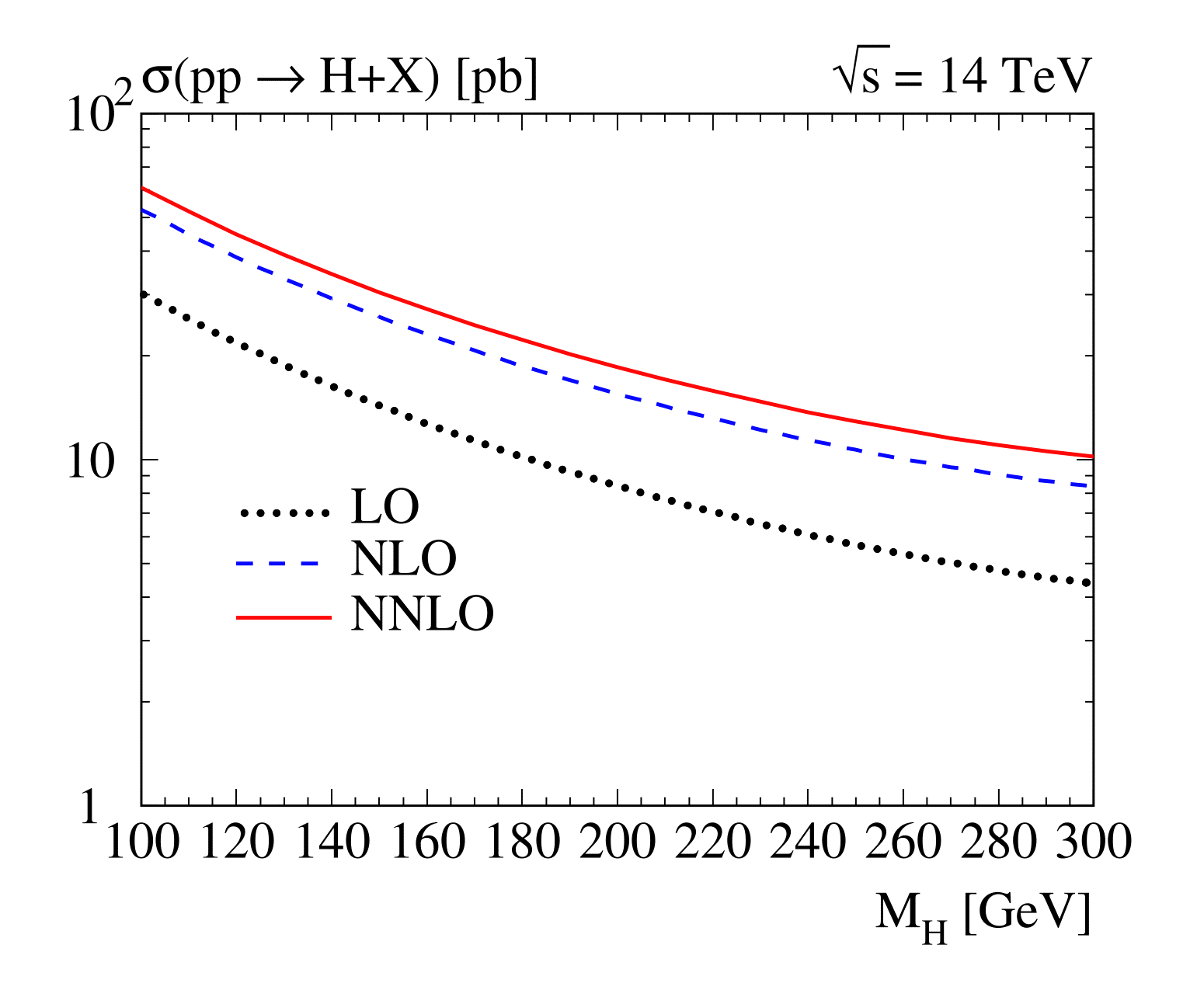
The cross section for Higgs production at NLO, using CTEQ6M pdfs, as a function of its mass is shown below. The largest production mechanism is gg fusion, through a top quark loop. The branching ratios for the Standard Model Higgs decay, as a function of its mass are also shown below.
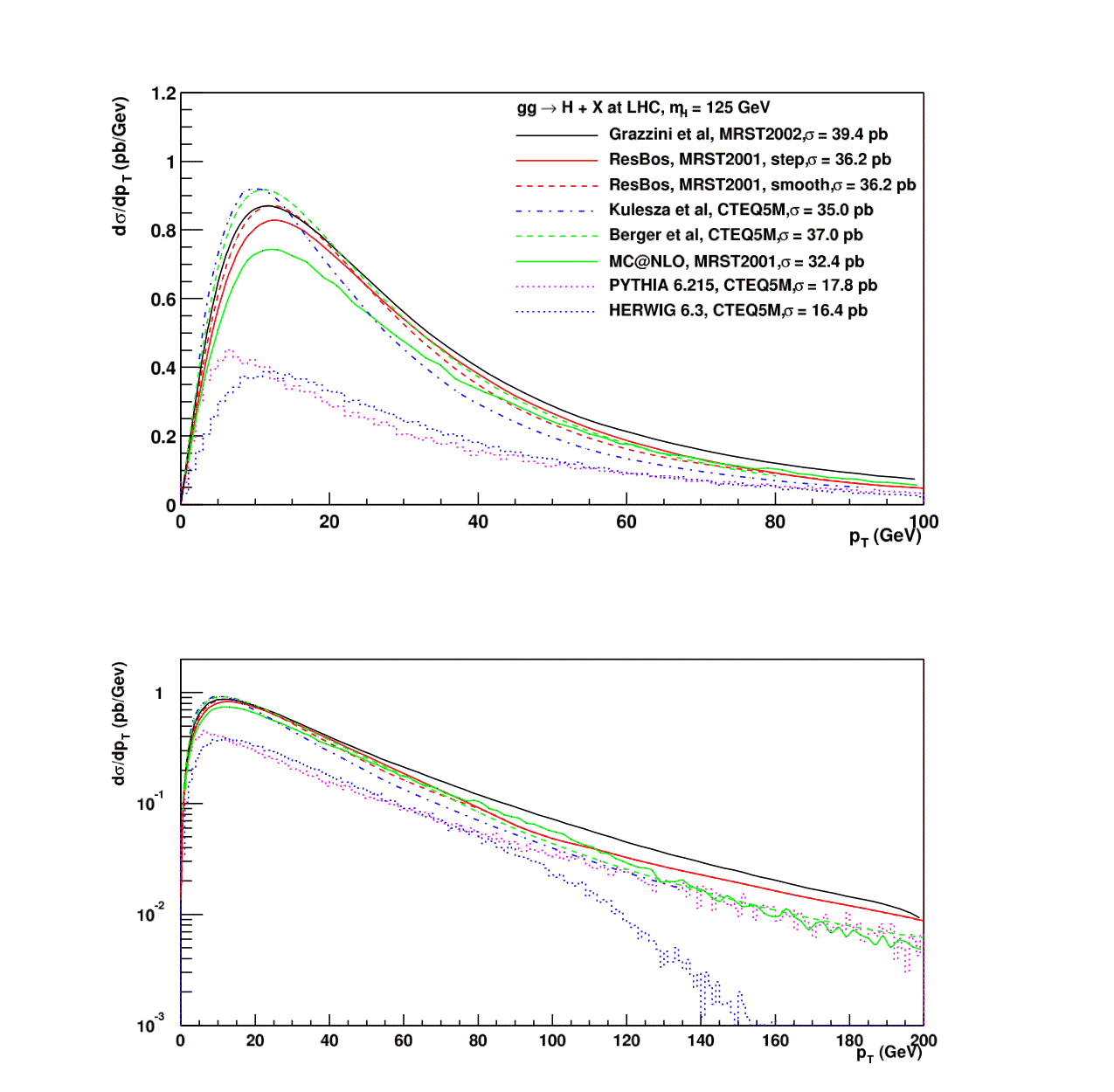
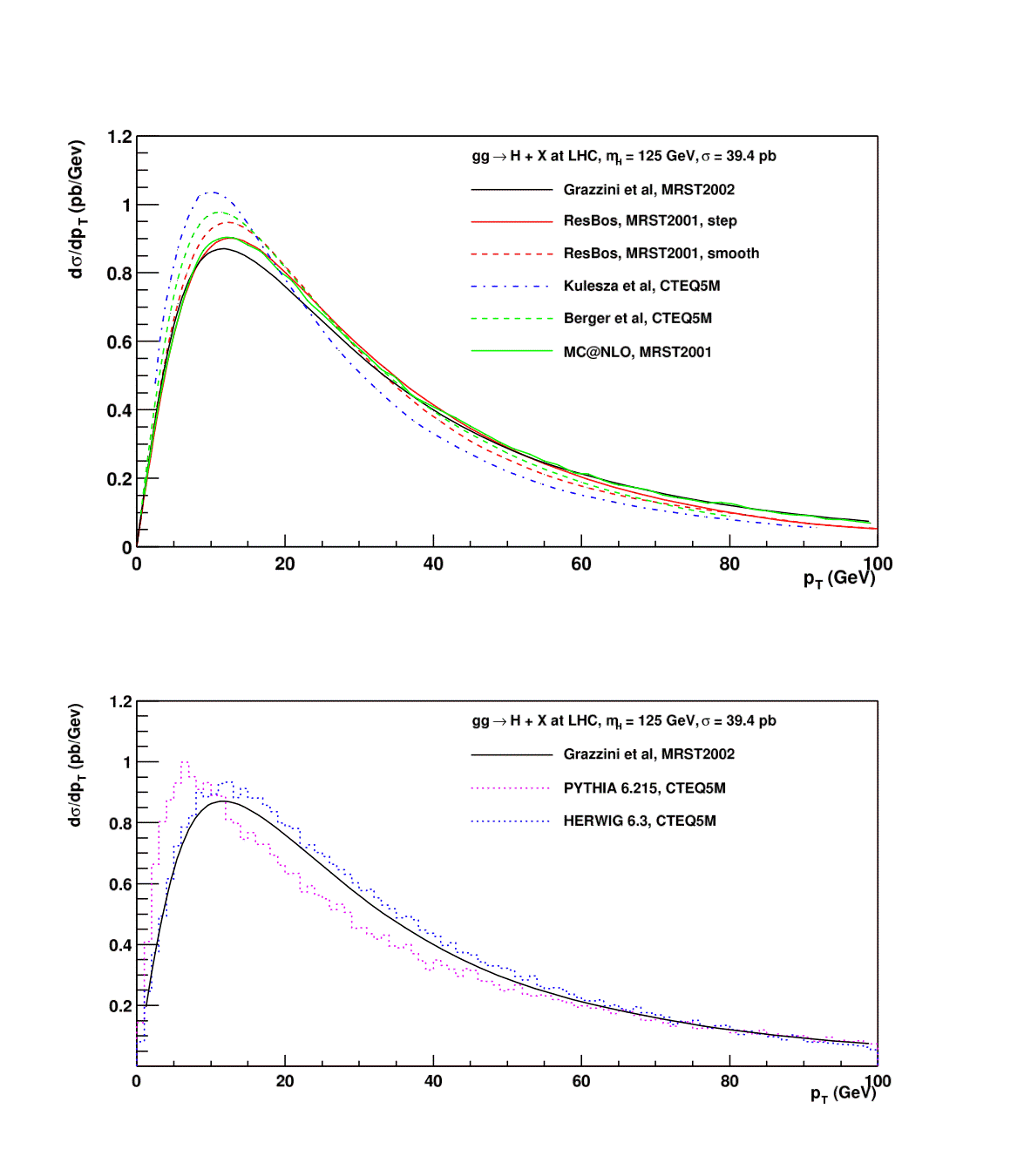
The kinematics for Higgs production are an important component for LHC searches. A comparison of various predictions for the Higgs transverse momentum distribution (for the gg subprocess) are shown below. The Higgs pT distribution peaks significantly higher than does the similar distribution for the Z boson due to the larger color factor for the initial state gluons and to the differences between the gluon and quark splitting functions. The parton shower Monte Carlos do a reasonable job in describing the shape of the pT distribution, but not its normalization.
A link to the ResBos program for calculation of Higgs kinematics can be found here.
Higgs physics on the back of an envelope
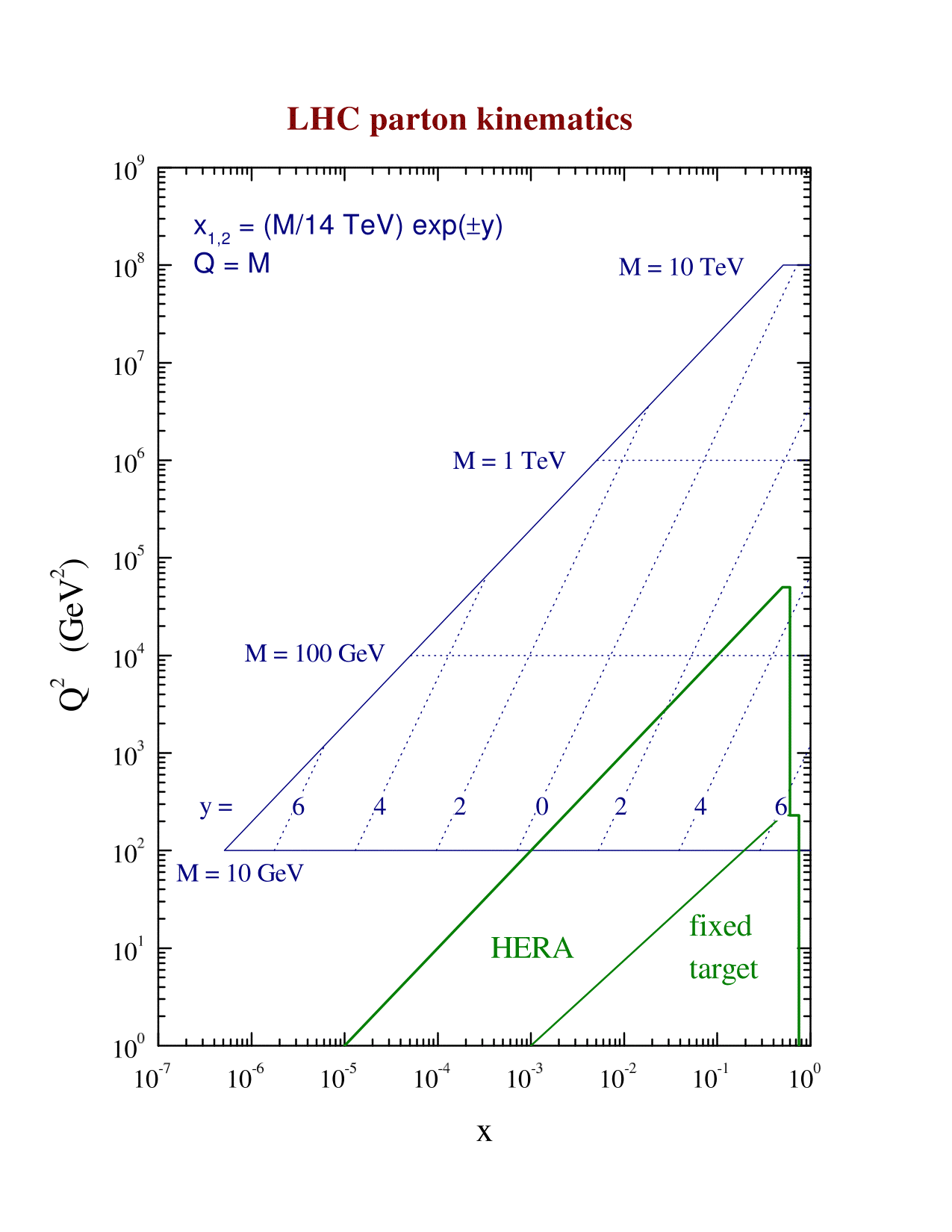
Estimating the cross sections and related quantities for Higgs production does not necessarily require running programs. Estimates accurate to within a few tens of percent should be possible with 'back-of-the-envelope' types of calculations. The pdf luminosity plots for the LHC are shown below. The gg luminosity is given by the blue curve. The LO cross section for Higgs production is shown below to the right.
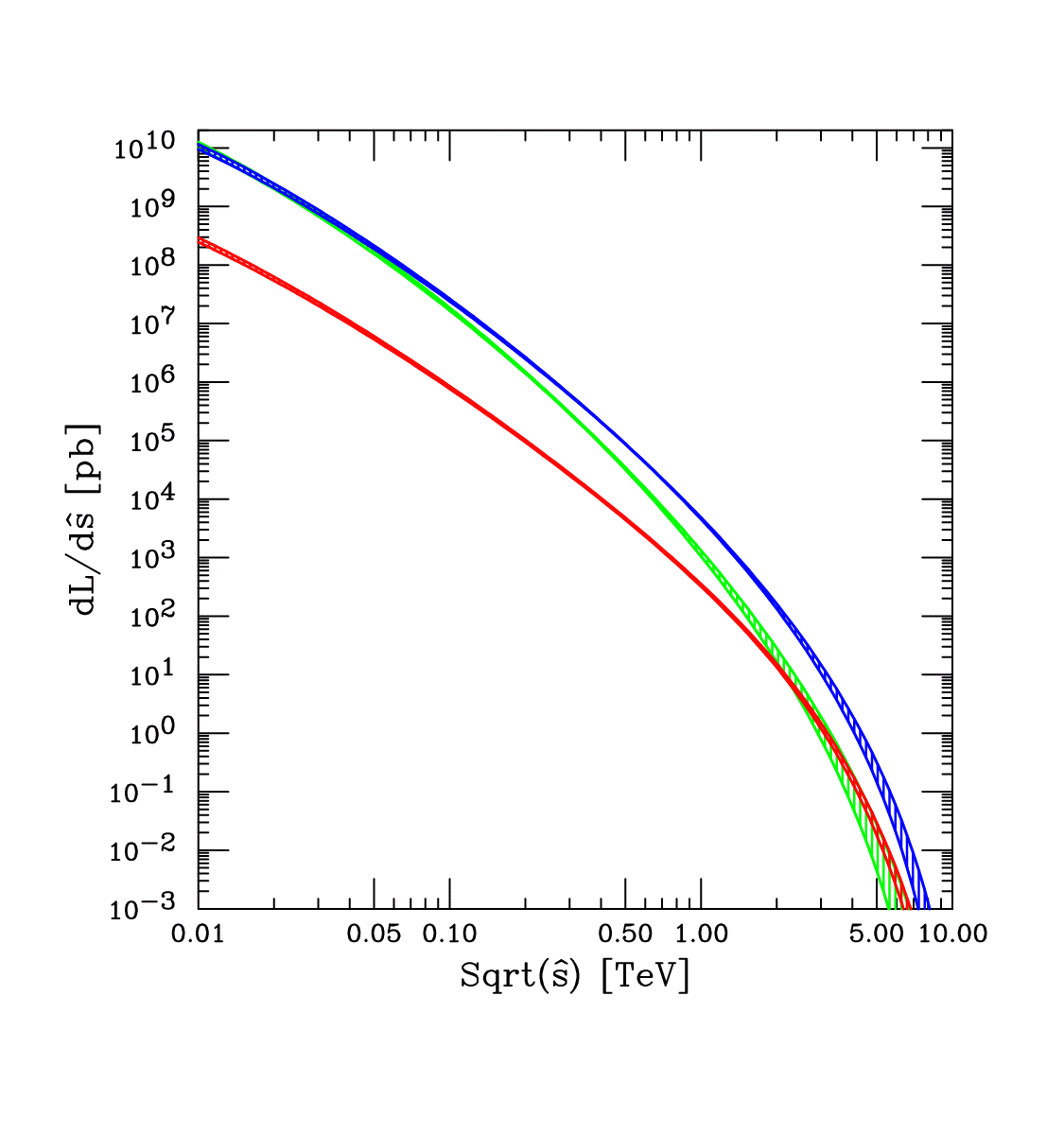

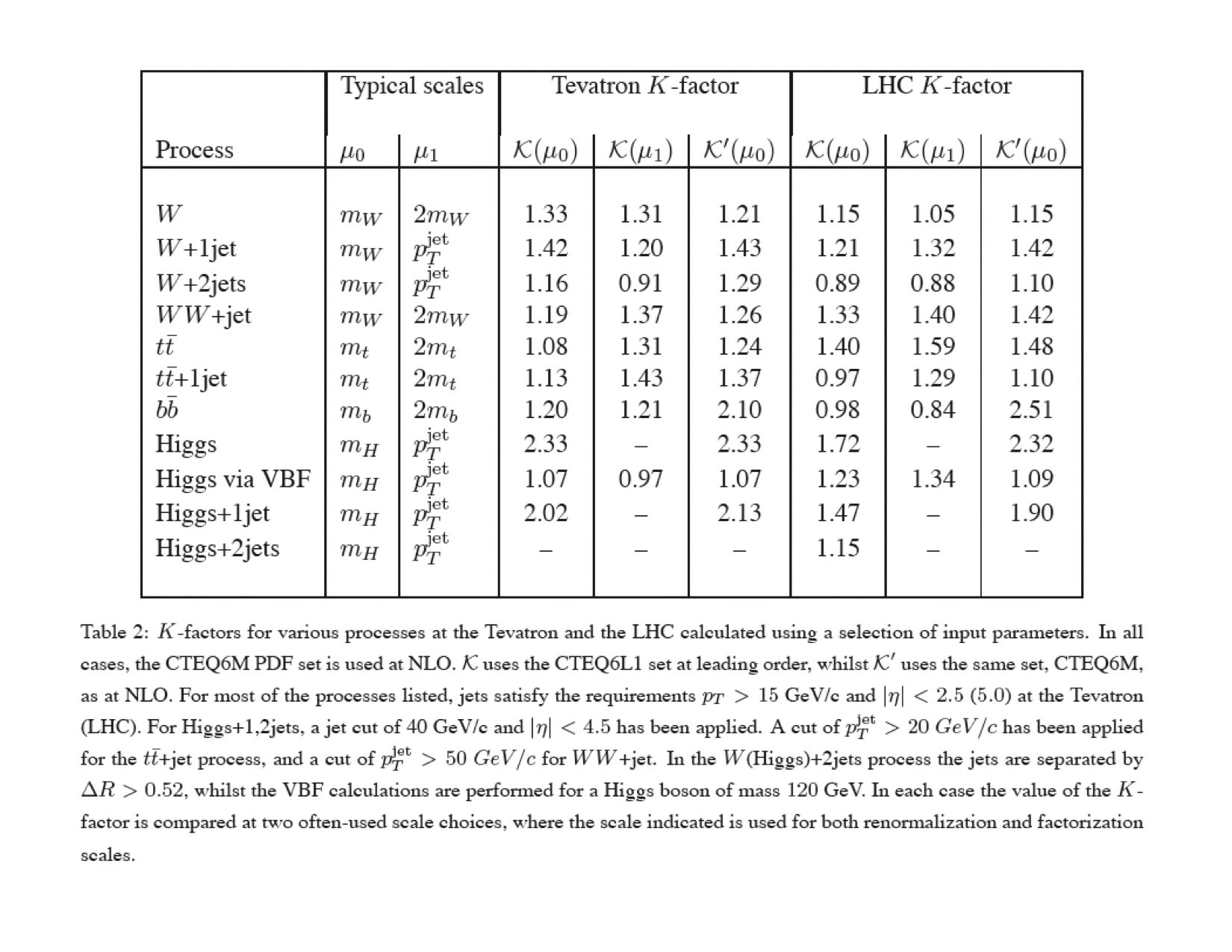
For example, for a Higgs mass of 120 GeV, the gg pdf luminosity is ~1E7pb. The Higgs sub-process cross section (at LO) at 120 GeV is 2E-06 pb, leading to a prediction for the Higgs cross section of 20 pb. The K-factor for Higgs production at the LHC can be read from the table below as 2.3 leading to a prediction at NLO as 46 pb, in agreement with the plot showon at the top of the page.
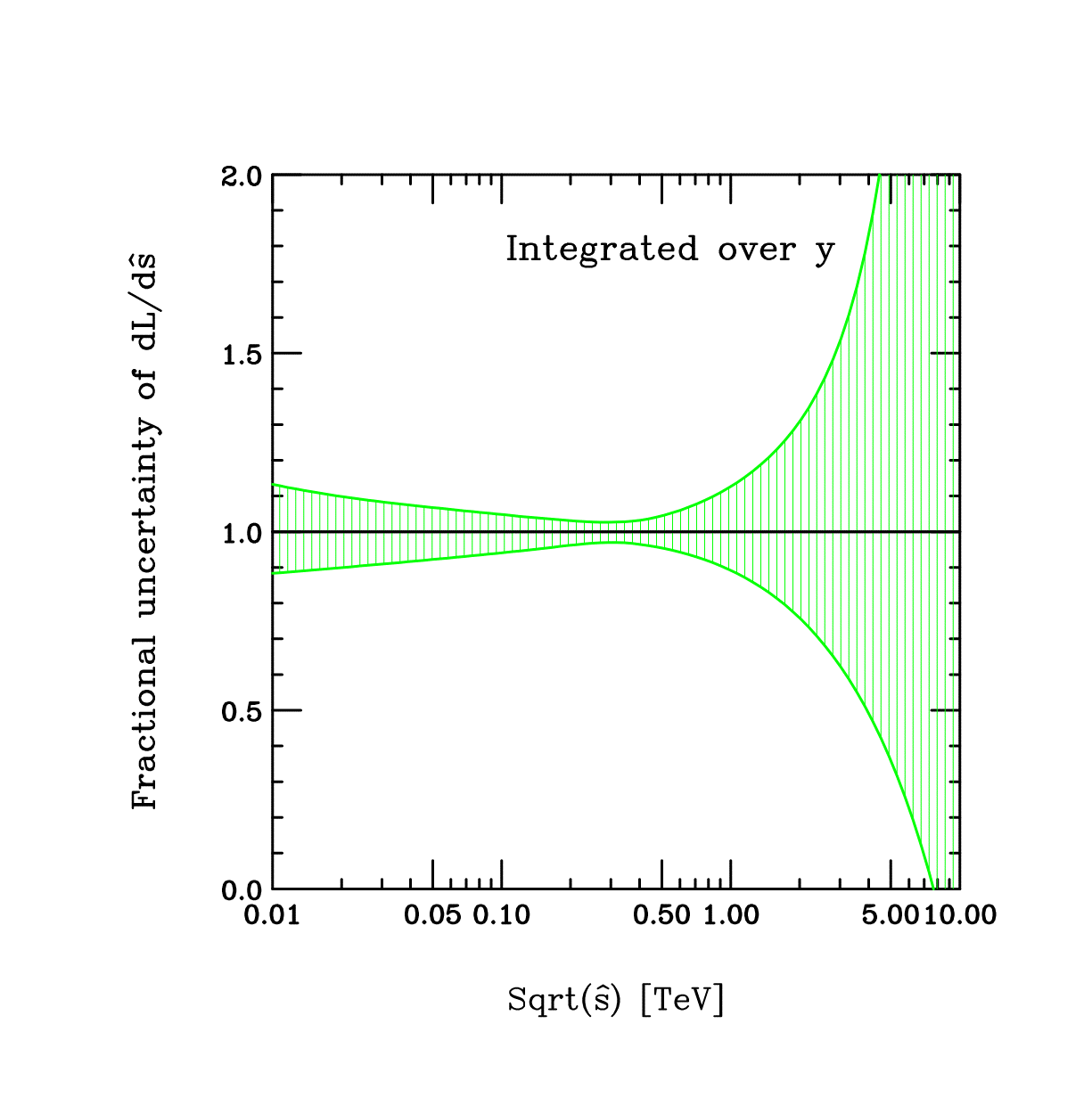
The pdf luminosity for Higgs production through gg production can be estimated from the figure below. For low mass Higgs production, the pdf uncertainty is less than 5%. The pdf correlations are shown on the lower right. Here we might also make available some pdf correlation tools.

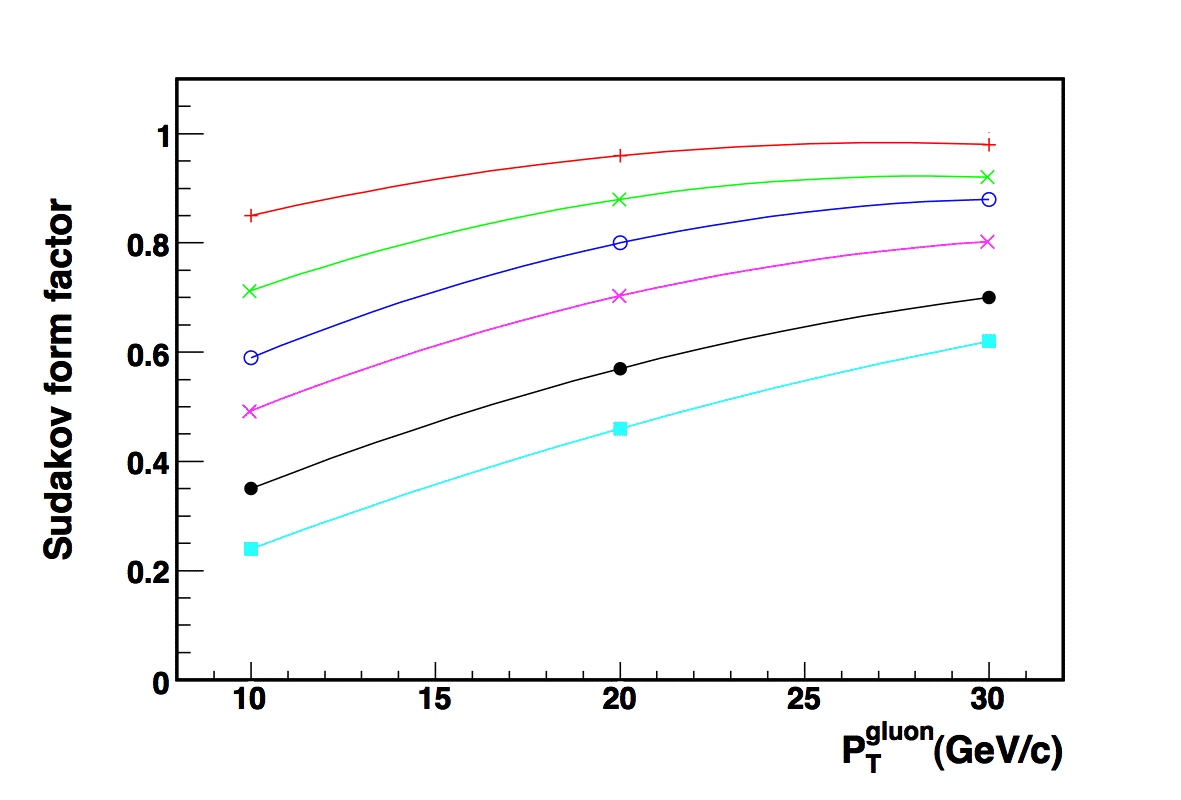
The initial state Sudakov form factor for one of the gluons producing the Higgs can be read from the plot shown below. The Sudakov form factors (for Q=100 GeV) are for x values of (top to bottom)
0.3,0.1,0.03,0.01, 0.001,0.0001. Production of a low mass Higgs involves initial state gluons with x values on the order of 0.01 (the purple curve). The Sudakov form factor for emitted
gluons on the order of 20 GeV is ~0.7, i.e. there is a probability of 0.3 of emitting such a gluon. The probability of neither initial state gluon emitting a gluon of 20 GeV or greater is
0.7*0.7, or ~0.5. Using Poisson statistics, the average jet multiplicity (for transverse momenta > 20 GeV) is 0.7.
The cross section for Higgs production at NLO, using CTEQ6M pdfs, as a function of its mass is shown below. The largest production mechanism is gg fusion, through a top quark loop. The branching ratios for the Standard Model Higgs decay, as a function of its mass are also shown below.


The kinematics for Higgs production are an important component for LHC searches. A comparison of various predictions for the Higgs transverse momentum distribution (for the gg subprocess) are shown below. The Higgs pT distribution peaks significantly higher than does the similar distribution for the Z boson due to the larger color factor for the initial state gluons and to the differences between the gluon and quark splitting functions. The parton shower Monte Carlos do a reasonable job in describing the shape of the pT distribution, but not its normalization.
A link to the ResBos program for calculation of Higgs kinematics can be found here.


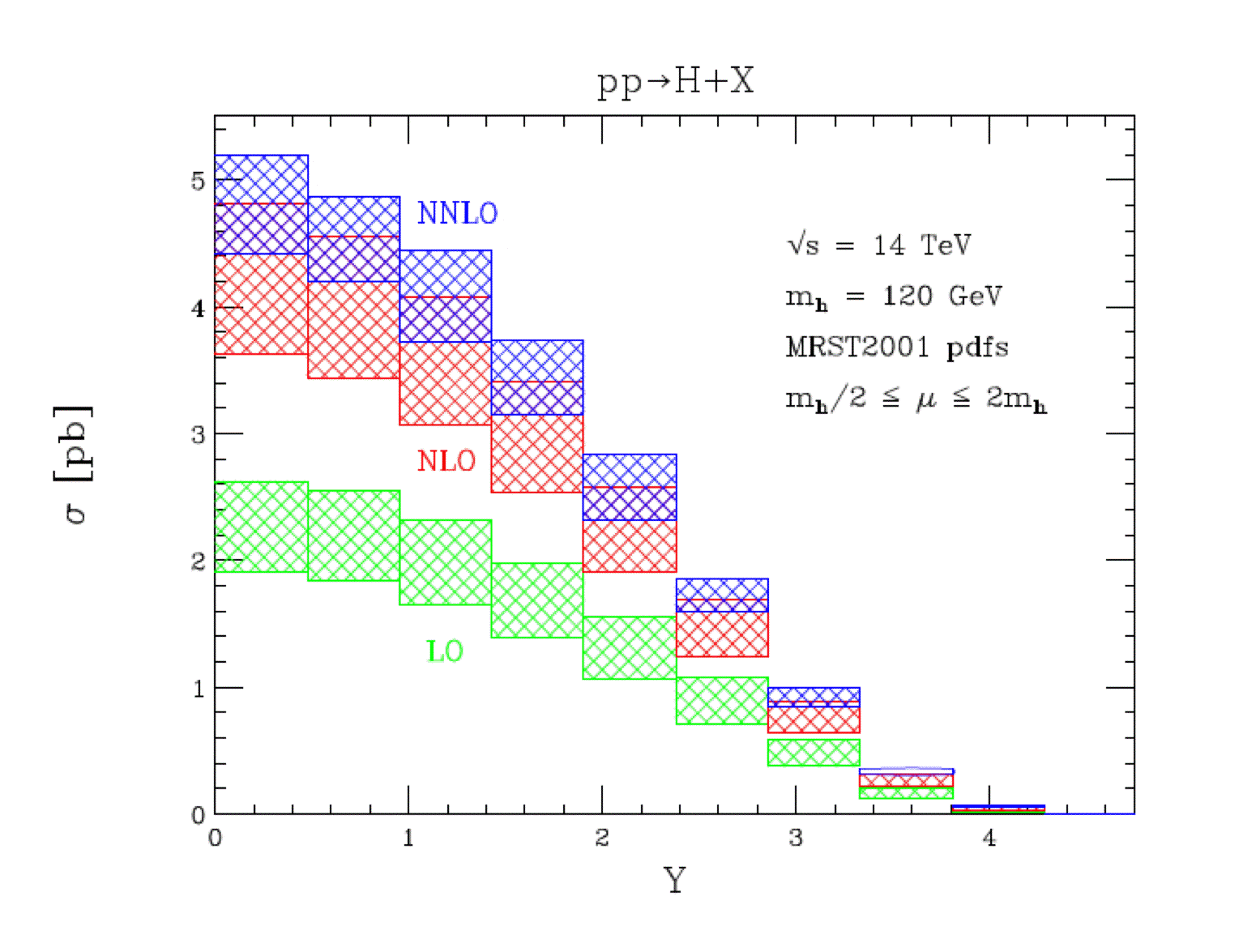
The cross section for the production
of a 120 GeV Higgs is shown at LO, NLO and NNLO below. There is a
significant K-factor in going from LO to NLO, with a smaller additional
normalization from NLO to NNLO. The K-factor is essentially independent
of the Higgs rapidity.The scale dependence of the cross section is also
shown in the figure on the right.


As part of the CTEQ4LHC exercise,
Higgs cross sections were generated for the LHC using the following
standard parameters:
PDFs: CTEQ6.6, CTEQ6L1, CTEQ modified LO pdf's
Order of calculations: LO, NLO, NNLO, NNLO+NNLL
.
.
.
Total cross section predictions for the gg subprocess are shown in the table below, at NLO and LO, with scales of mHiggs and mHiggs/2 and with cteq6.6, cteq6l1 and modified LO pdf's. The relevant K-factor (NLO/LO is shown in parentheses next to the LO cross section. The calculations were performed with MCFM.
Here are some cross section plots for production of a 120 GeV mass Higgs through gg fusion.

Here is a cross section table for the rapidity distribution for a 120 GeV Higgs. Ultimately, this will be linkable, rather than appearing on the main page.
ROOT ntuples for each of the predictions above can be found below, along with a sample ROOT analysis script. Since the ntuples may be quite large, we'll have to find the best way of making
them available.
Here we can link to pages on other Higgs cross section programs, VBF production, Higgs + 1 jet, Higgs + 2 jets, etc.
PDFs: CTEQ6.6, CTEQ6L1, CTEQ modified LO pdf's
Order of calculations: LO, NLO, NNLO, NNLO+NNLL
.
.
.
Total cross section predictions for the gg subprocess are shown in the table below, at NLO and LO, with scales of mHiggs and mHiggs/2 and with cteq6.6, cteq6l1 and modified LO pdf's. The relevant K-factor (NLO/LO is shown in parentheses next to the LO cross section. The calculations were performed with MCFM.
| order |
NLO |
NLO |
LO |
LO |
LO |
LO |
LO |
LO |
| PDF |
cteq6.6 |
cteq6.6 |
cteq6.6 |
cteq6.6 |
cteq6l1 |
cteq6l1 |
mod LO |
mod LO |
| scale |
mHiggs |
mHiggs/2 |
mHiggs |
mHiggs/2 |
mHiggs |
mHiggs/2 |
mHiggs |
mHiggs/2 |
| sigma (fb) mHiggs=120 GeV |
36340 |
42455 |
15830 (2.30) |
18190 (2.43) |
||||
| sigma (fb) mHiggs=200 GeV |
12815 |
15020 |
5865 (2.18) |
|||||
| sigma (fb) mHiggs=300 GeV |
5070 |
5955 |
2395 (2.12) |
2925 (2.04) |
||||
| sigma (fb) mHiggs=400 GeV |
Here are some cross section plots for production of a 120 GeV mass Higgs through gg fusion.

Here is a cross section table for the rapidity distribution for a 120 GeV Higgs. Ultimately, this will be linkable, rather than appearing on the main page.
| order |
NLO |
NLO |
LO |
LO |
LO |
LO |
LO |
LO |
| PDF |
cteq6.6 |
cteq6.6 |
cteq6.6 |
cteq6.6 |
cteq6l1 |
cteq6l1 |
mod LO |
mod LO |
| scale |
120 GeV |
60 GeV |
120 GeV |
60 GeV |
120 GeV |
60 GeV |
120 GeV |
60 GeV |
| |y| range |
sigma(fb) |
sigma(fb) |
sigma(fb) |
sigma(fb) |
||||
| 0.0-0.2 |
3.41E3 |
3.93E3 |
1.47E3 |
1.67E3 |
||||
| 0.2-0.4 |
3.37E3 |
3.96E3 |
1.46E3 |
1.66E3 |
||||
| 0.4-0.6 |
3.29E3 |
3.90E3 |
1.43E3 |
1.62E3 |
||||
| 0.6-0.8 |
3.23E3 |
3.71E3 |
1.38E3 |
1.58E3 |
||||
| 0.8-1.0 |
3.10E3 |
3.49E3 |
1.32E3 |
1.51E3 |
||||
| 1.0-1.2 |
2.80E3 |
3.43E3 |
1.26E3 |
1.44E3 |
||||
| 1.2-1.4 |
2.70E3 |
3.08E3 |
1.17E3 |
1.34E3 |
||||
| 1.4-1.6 |
2.52E3 |
3.08E3 |
1.08E3 |
1.24E3 |
||||
| 1.6-1.8 |
2.21E3 |
2.38E3 |
9.78E2 |
1.13E3 |
||||
| 1.8-2.0 |
2.02E3 |
2.47E3 |
7.58E2 |
1.01E3 |
||||
| 2.0-2.2 |
1.71E3 |
2.01E3 |
6.49E2 |
8.78E2 |
||||
| 2.2-2.4 |
1.49E3 |
1.73E3 |
5.36E2 |
7.53E2 |
||||
| 2.4-2.6 |
1.21E3 |
1.41E3 |
4.30E2 |
6.26E2 |
||||
| 2.6-2.8 |
9.80E2 |
1.18E3 |
3.37E2 |
5.04E2 |
||||
| 2.8-3.0 |
7.49E2 |
8.50E2 |
2.51E2 |
3.95E2 |
||||
| 3.0-3.2 |
5.58E2 |
6.88E2 |
1.80E2 |
2.98E2 |
||||
| 3.2-3.4 |
4.16E2 |
4.81E2 |
1.20E2 |
2.13E2 |
||||
| 3.4-3.6 |
2.54E2 |
3.08E2 |
7.47E1 |
1.45E2 |
||||
| 3.6-3.8 |
1.69E2 |
2.01E2 |
4.26E1 |
9.15E1 |
||||
| 3.8-4.0 |
8.97E1 |
1.03E2 |
2.07E1 |
5.36E1 |
||||
| 4.0-4.2 |
4.58E1 |
6.02E1 |
7.51E0 |
2.73E1 |
||||
| 4.2-4.4 |
1.77E1 |
2.16E1 |
1.36E0 |
1.06E1 |
||||
| 4.4-4.6 |
3.40E0 |
4.29E0 |
2.59E-2 |
2.10E0 |
||||
| 4.6-4.8 |
7.19E-2 |
1.18E-1 |
ROOT ntuples for each of the predictions above can be found below, along with a sample ROOT analysis script. Since the ntuples may be quite large, we'll have to find the best way of making
them available.
| order |
NLO |
NLO |
LO |
LO |
LO |
LO |
LO |
LO |
| PDF |
cteq6.6 |
cteq6.6 |
cteq6.6 |
cteq6.6 |
cteq6l1 |
cteq6l1 |
mod LO |
mod LO |
| scale |
mHiggs |
mHiggs/2 |
mHiggs |
mHiggs/2 |
mHiggs |
mHiggs/2 |
mHiggs |
mHiggs/2 |
| mHiggs=120 GeV |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
| mHiggs=200 GeV |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
| mHIggs=300 GeV |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
| mHiggs=400 GeV |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
ntuple |
Here we can link to pages on other Higgs cross section programs, VBF production, Higgs + 1 jet, Higgs + 2 jets, etc.
Higgs physics on the back of an envelope
Estimating the cross sections and related quantities for Higgs production does not necessarily require running programs. Estimates accurate to within a few tens of percent should be possible with 'back-of-the-envelope' types of calculations. The pdf luminosity plots for the LHC are shown below. The gg luminosity is given by the blue curve. The LO cross section for Higgs production is shown below to the right.


For example, for a Higgs mass of 120 GeV, the gg pdf luminosity is ~1E7pb. The Higgs sub-process cross section (at LO) at 120 GeV is 2E-06 pb, leading to a prediction for the Higgs cross section of 20 pb. The K-factor for Higgs production at the LHC can be read from the table below as 2.3 leading to a prediction at NLO as 46 pb, in agreement with the plot showon at the top of the page.

The pdf luminosity for Higgs production through gg production can be estimated from the figure below. For low mass Higgs production, the pdf uncertainty is less than 5%. The pdf correlations are shown on the lower right. Here we might also make available some pdf correlation tools.


The initial state Sudakov form factor for one of the gluons producing the Higgs can be read from the plot shown below. The Sudakov form factors (for Q=100 GeV) are for x values of (top to bottom)
0.3,0.1,0.03,0.01, 0.001,0.0001. Production of a low mass Higgs involves initial state gluons with x values on the order of 0.01 (the purple curve). The Sudakov form factor for emitted
gluons on the order of 20 GeV is ~0.7, i.e. there is a probability of 0.3 of emitting such a gluon. The probability of neither initial state gluon emitting a gluon of 20 GeV or greater is
0.7*0.7, or ~0.5. Using Poisson statistics, the average jet multiplicity (for transverse momenta > 20 GeV) is 0.7.

