

Capacitors in parallel and series
Here we discuss the effective capacitance of connecting two capacitors together. In the figure on the left the capacitors are connected in parallel, while in the right-hand-side figure the capacitors are connected in series.
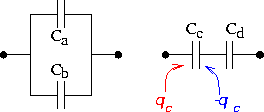
First, let us consider the left-hand figure where the two capacitors are in parallel. The charge sucked into the left-hand element is:
![]() ,
,
where V is the voltage across both elements. Remember that the voltage along a conductor does not change, and that a wire is a conductor, so both capacitors have the same voltage drop across them. From inspection of the equation above, one sees that the effective capacitance, C is:
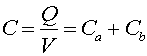
This makes sense as the capacitance is e0A/d and putting two identical capacitors side by side should look like one capacitor with double the area and therefore double the capacitance.
Next, consider the situation to the right, where the capacitors are in series. Remember that when we refer to the charge on the plate, it is the charge on one side, as the opposite charge is sucked off the other plate. Thus, the charge qd = qc.For two capacitors in series, the charges are identical, but the voltages are different. The sum of the voltage drops across the two capacitors must equal the net voltage drop V.
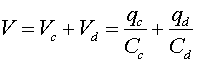
Using the fact that the effective charge Q sucked into the element equals qc which equals qd, we see that:
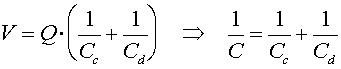
Thus, we see that for capacitors in parallel, the capacitances add, while for capacitors in series, their inverses add. For resistors, we will find that the opposite is true.