Maxwell's equations and light
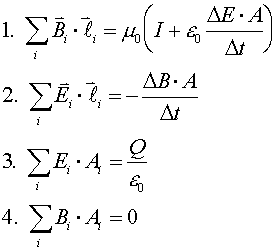Light is an electromagnetic wave. To explain this, we consider Maxwell's
equations, the four equations that describe all of electricity and magnetism. The first
equation is Ampere's law, only that the second term on the right-hand-side is new. The
second equation is Lenz's law. The third equation is Gauss's law and expresses the fact
that electric field lines begin and end only at charges. The fourth equation is the
magnetic equivalent of Gauss's law, expressing tha fact that magnetic field lines never
begin or end.
After a bit of non-trivial differential calculus one can show that both the electric and magnetic field obey wave equations. The speed c of an electromagnetic wave is given by: c2 =1/(e0m0) = 2.998 m/s.
The details of an electromagnetic wave are fairly complicated. If the wave moves in z-direction, the electric field oscillates in the plane perpendicular to the z-axis. The magnetic field also oscillates and is perpendicular to both the magnetic and electric fields. If the electric field is oscillating in the x-direction, we say the wave is polarized along the x-axis. The figure below illustrates the behavior of an electromagnetic wave which is polarized along the x-axis.
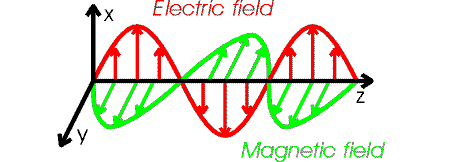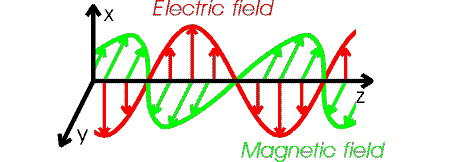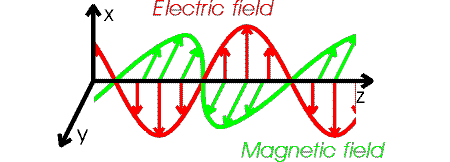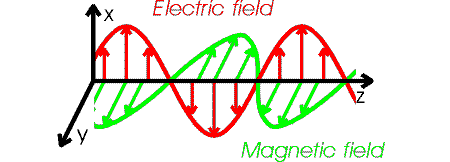
The forms of the electric and magnetic field in the wave are:
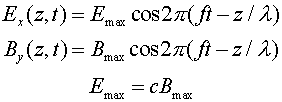
where the frequency and wavelength are related by c = fl.