

Circular motion in a magnetic field
Charged particles in a magnetic field feel a force perpendicular to their velocity. Since their movement is always perpendicular to the force, magnetic forces do no work and the particle's velocity stays constant. Since the force is F = qvB in a constant magnetic field, a charged particle feels a force of constant magnitude always directed perpendicular to its motion. The result is a circular orbit.
The diagram below represents constant magnetic field for two cases. On the left the magnetic field is pointed into the page while on the right the field lines are exiting the page. The crosses indicate the field is directed into the page. One can think of this as the tail of a feather as it travels away from view, whereas the dots represent the point of the approaching arrow. The fact that the field is uniform is indicated by the equal spacing of the arrows. Using the right-hand rule one can see that a positive particle will have the counter-clockwise and clockwise orbits shown below.
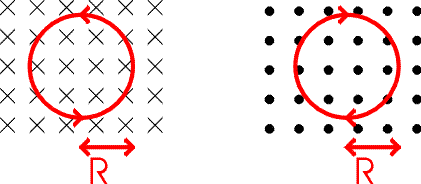
The radius of the orbit depends on the charge and velocity of the particle as well as the strength of the magnetic field. The acceleration of a particle in a circular orbit is:
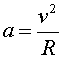
Using F = ma, one obtains:

Thus the radius of the orbit depends on the particle's momentum, mv, and the product of the charge and strength of the magnetic field. Thus by measuring the curvature of a particle's track in a known magnetic field, one can infer the particle's momentum if one knows the particle's charge. A device which works in such a fashion is called a magnetic spectrometer. Most high-energy physics experiments use exactly such devices, even though the particle's have so much momentum that they never circle but only curve a few degrees from their straight line trajectories.