

The Stefan Boltzmann Law of Radiation
From Physics 231 we know that systems at a higher temperature are composed of particles with a higher kinetic energy. This is true for thermalized photons as well. For a gas of non-relativistic particles, the average energy per particle was (3/2)kT. For photons the average energy per photon will be kT, but with photons a second questions arises: How many photons are there?
Since the average energy per photon is proportional to the temperature, and the energy of a photon is inversely related to it's wavelength, E = hc/l, one can see that the spectrum of light from a hot object is related to it's temperature.
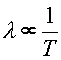
From the Heisenberg uncertainty principle we can determine that the number of photon states with momentum less than pmax and within a three dimensional volume V is proportional to
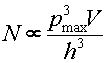 ,
,
where h is Planck's constant. Since the characteristic cutoff of the momentum pmax is proportional to the temperature and the average energy is also proportional to the temperature, the number of photons per volume is proportional to T4. The rate at which energy leaves the hot volume is proportional to the surface area of the volume, the velocity per photon, the number of photons per cubic volume and the average energy per photon. Some quantum mechanics reveals the energy emitted per time, Stefan-Boltzmann Law:
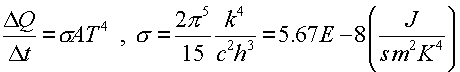
The Stefan-Boltzmann constant s was used in Physics 231, but here we see that it can be found in terms of fundamental constants including Planck's constant. Historically, this was how Planck came upon the constant.