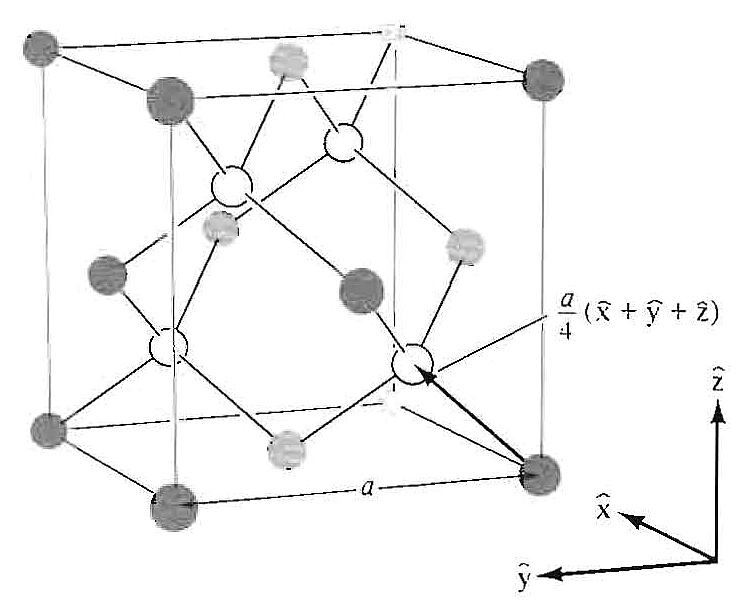

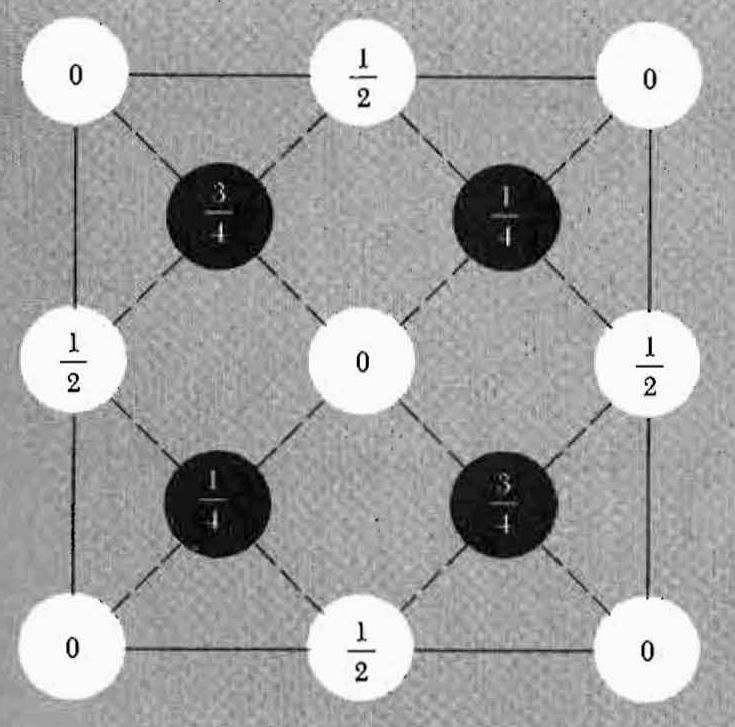
1. (a) (1 pt.) Prove that the diamond structure is invariant under an inversion in the midpoint of any nearest neighbor bond.
(b) (2 pt.) Show that the diamond structure is not invariant under inversions in any points, which are not midpoints of bonds between sublattices.
2. (2 pt.) The unit cell of a tetragonal crystal is a rectangular block with sides of lengths a,a,b, respectively. What is the spacing between planes characterized by Miller indices (h,k,l)? Write down the Bragg condition for diffraction of X-rays with wavelength λ through an angle 2θ.
3. (6 pt.) Work out the position of the first four reflections from diamond in a powder experiment using λ= 0.077 nm X-rays. (The nearest neighbor carbon-carbon separation is 0.154 nm. The diamond structure as presented in Figure 4.18 in Ashcroft and Mermin, and in Figure 1-24 in Kittel is reproduced below.) Show that if the charge distribution on the carbon atoms were spherically symmetric, then the (222) reflection would be forbidden. By placing point charges between the carbon atoms to simulate the covalent bonding, show that the (222) reflection is allowed and so gives a direct measure of the bond charge. (Note the convention that Miller indices refer to the underlying simple cubic Bravais lattice of the diamond lattice structure.)


