Interactive guide to diffraction ..

Interactive Tutorial about Diffraction
Anomalous dispersion: centrosymmetric structure

Anomalous dispersion
Centric structure
Acentric structure

This set of examples shows the effect of anomalous dispersion on the Fourier transform. Both, for a centrosymmetric as well as an acentric structure, the Fourier transform is calculated with and without taking anomalous dispersion into account. A simple 1-D structure has been chosen, since the effects are small. The one dimensional representation of the results allows a better insight into the subtle differences.

Anomalous dispersion can be characterized by changing the scattering factor. An additional real and imaginary term modifies the usual atom form factor:

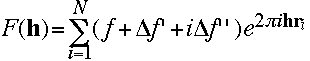
The first image shows the centrosymmetric structure. It consists of two different atoms, Oxygen and Zirconium at:

Name	x	y	z
Zirconium	0.00	0.00	0.00
Oxygen	0.15	0.00	0.00
Oxygen	-0.15	0.00	0.00
Oxygen	0.50	0.00	0.00
Oxygen	-0.50	0.00	0.00

In the graphical representation, the Zirconium atom is blue and the oxygen atoms are red. The effects of anomalous dispersion are weak. In this example, they have been enhanced by setting f' and f" to large values: f=40.0, f'=-15.0 and f''=13.5. Now lets calculate the Fourier transform of this molecule. In this and all following images the Fourier transform calculated without anomalous dispersion is shown in blue, the Fourier transform with anomalous dispersion is red. The pictures below show from left to right the calculated intensity, the real and the imaginary part of the structure factor. To see the small differences more clearly, click on the pictures to get a full screen view.

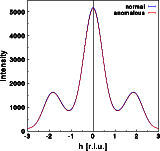
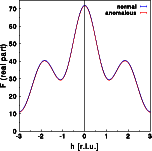
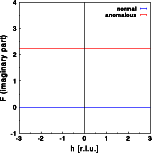
The intensity does change very slightly, as can be seen by the differences between the blue and red curve. The differences are, however, identical for h and -h. Friedel's law still holds for a centrosymmetric structure, even in the presence of anomalous scattering. The real part of the Fourier transform shows hardly any difference at all. Again, the changes are identical for h and -h. The imaginary part of the structure calculated without anomalous dispersion is zero at all h (blue line). The imaginary part deviates from zero. In this simple example, it is constant since the anomalous scatterer (Zr) is at the center of real space. This, however, would not be the case if the Zr were at a general position within the unit cell! The imaginary part has been plotted at the same scale as the real part. You can see that the changes of the imaginary part are small compared to the absolute value of the real part. Let us finally have a look at the phase distribution:

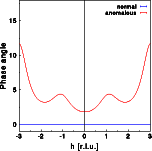
The phase angle of the centrosymmetric structure is zero or 180 for all h in the absence of anomalous dispersion. If anomalous dispersion is present (red curve), the phase angle of a centrosymmetric structure is allowed to take on general values as well. The phase angle for -h is always identical to that of h.