Anomalous dispersion
Centric structure
Acentric structure

Goto
Contents

Name	x	y	z
Zirconium	0.00	0.00	0.00
Oxygen	0.025	0.00	0.00
Oxygen	0.150	0.00	0.00
Oxygen	0.600	0.00	0.00

In the graphical representation, the Zirconium atom is blue and the oxygen atoms are red. The effects of anomalous dispersion are weak. In this example, they have been enhanced by setting f' and f" to large values: f=40.0, f'=-15.0 and f''=13.5. Now lets calculate the Fourier transform of this molecule. In this and all following images the Fourier transform calculated without anomalous dispersion is shown in blue, the Fourier transform with anomalous dispersion is red. The pictures below show from left to right the calculated intensity, the real and the imaginary part of the structure factor. To see the small differences more clearly, click on the pictures to get a full screen view.

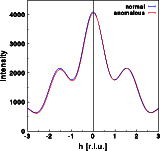
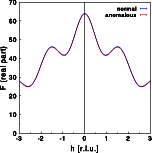
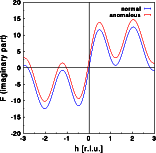
The intensity does change very slightly, as can be seen by the differences between the blue and red curve. Contrary to the centrosymmetric example, the differences are no longer identical for h and -h. Friedel's law does not hold for an acentric structure in the presence of anomalous scattering. Note that the intensity at h=-2 are weaker in case of anomalous dispersion, and almost identical for h=+2.The real part of the Fourier transform shows hardly any difference at all. Again, the changes are no longer identical for h and -h.For the imaginary part of the structure calculated without anomalous dispersion I(h) = -I(-h), as can be seen in the blue curve. As for the centrosymmetric case, the imaginary part gets a constant shift since the zirconium is at the center of real space. This, however, would not be the case if the Zr were at a general position within the unit cell! A more general modification of the imaginary part would result. Now, I(h) is no longer identical to -I(-h). Let us finally have a look at the phase distribution:

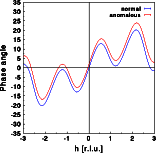
The phase angle of the acentric structure assumes any value between -180 and +180 degrees. Without anomalous dispersion PHI(h) = -PHI(-h). In the presence of anomalous dispersion this relationship does not hold anymore.