Interactive guide to diffraction ..

Interactive Tutorial about Diffraction
Convolution I: Convolution theorem

Convolution
Convolution theorem
Square box
Rectangular box
Circular box
Box at 45 degrees

This example illustrates the effect of the convolution theorem. The real space electron density distribution of a single atom (left image) is convoluted with a finite train of five point scatterers (middle image) to form a finite sized crystal (right image). Click on the pictures to get a full screen version.

Now we calculate the corresponding Fourier transform in one dimension. The left image shows the Fourier transform of the single atom, the middle image the Fourier transform of the finite train of point scatterers. Since the electrons of atoms are distributed throughout a finite volume, the waves scattered by different parts of the atom contribute with different phases to the resulting wave. The (in part) destructive interference lowers the intensity of the scattered wave. Thus, the Fourier transform of this electron density distribution drops off to higher scattering vectors.

In contrast, the Fourier transform of the finite train of point scatterers does not decrease with increasing scattering vector. Multiplication of the last two Fourier transforms gives the right image, which is identical to the image produced directly by the Fourier transform of the finite crystal.

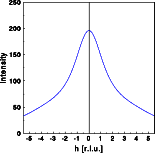
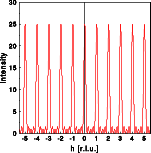
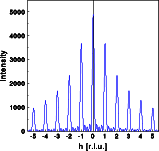
The Fourier transform of the finite train of point scatterers in itself is an example of the inverse to the convolution theorem, the multiplication theorem. The Fourier transform of an infinite lattice would be a reciprocal lattice without any subsidiary maxima. By multiplying the infinite lattice with a box shaped function, that is 1 inside and zero outside the box, a finite train is obtained. As a result each reciprocal lattice point is convoluted by the Fourier transform of the box function which results in the subsidiary maxima.