Interactive guide to diffraction ..

Interactive Tutorial about Diffraction
Convolution III: Rectangular box

Convolution
Convolution theorem
Square box
Rectangular box
Circular box
Box at 45 degrees

In order to illustrate the theorem further, lets limit the crystal by a rectangular box (left image). Again the reciprocal lattice results convoluted by the Fourier transform of a rectangular box (right image). Click on the pictures to get a full screen version.

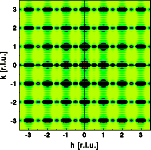
As expected, the Bragg reflections are convoluted by the Fourier transform of the shape function again. This time there are many subsidiary maxima along the vertical and few along the horizontal. Also the FWHM of the Bragg reflections is small along the vertical and large along the horizontal. These features represent the Fourier transform of the shape function.

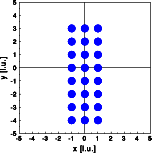
The box is simulated by filling the shape at random with a large number (800) of atoms (left image). The resulting electron density distribution fills the box fairly equally. Next the Fourier transform is calculated in a small section of reciprocal space near the origin. The calculated intensity distribution corresponds to the distribution of the subsidiary maxima observed in the Fourier transform above.

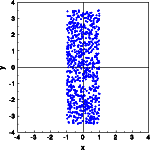
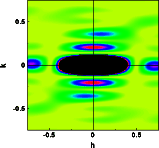
The deviations from orthorhombic symmetry are due to the limited statistics provided by the 800 atoms within the square box.