Interactive guide to diffraction ..

Interactive Tutorial about Diffraction
Phase problem I: Shift in real space

Phase problem
Shift in real space
Centrosymmetric vs. Acentric

Interactive examples
Single atom
Pair of atoms
One atom in unit cell
Two atoms in unit cell

In this exercise we look again at the Fourier transform of a single atom. The calculations are performed twice, once for the blue atom at the origin of real space and second for the red atom shifted to 0.5, 0, 0. Note that this is not a periodic crystal. The first image shows the two different positions.

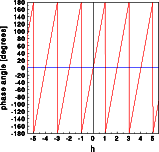
The Fourier transforms were calculated along a line through reciprocal space from -5.5,0,0 to +5.5,0,0. The left image shows the real(blue) and imaginary (red) part for the atom at 0,0,0. The corresponding intensities reduced by a factor of 10 are shown in green color. The middle image shows the corresponding values for the atom shifted in real space. The right image shows the phase of the wave scattered by the atom at 0,0,0 (blue) and the shifted atom (red).

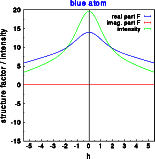
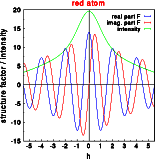
In the above left image the real part of the amplitude is positive, while the imaginary part is zero, as expected from a centrosymmetric structure. In the middle image, the Fourier transform of the atom shifted in real space, the real and the imaginary part oscillate. The resulting intensity, however, is identical in both cases! The information about the phase is lost. This marks a good opportunity to discuss the crystallographic phase problem.

The phase of the wave scattered by the atom at 0,0,0 (blue) is zero at all points in reciprocal space, as expected. With the atom at 0.5,0,0 (red), however, the phase oscillates between -180 and 180 degrees with a wave length of two reciprocal lattice units. Both structures are centrosymmetric, the only difference is the shift of origin by -0.5,0,0 ! A quick look at the properties of Fourier transforms reveals the cause. A real space shift results in multiplication with a phase factor in reciprocal space:

The complex exponential results in the phase factor shown in the top right image. The students will learn from this exercise:

Real space translation results in a reciprocal space phase oscillation
The intensity is invariant under a shift of origin ==> crystallographic phase problem
The phase of diffraction calculated for a crystal simulated in the computer depends on the position of the origin. Unless the center of symmetry of the real space structure is at 0,0,0 the resulting amplitudes are complex, even for a centrosymmetric structure.

Possible extensions of this exercise:

Have the students vary the real space shift, in order to show that the periodicity of the reciprocal phase oscillation is indeed 1/a.
Have the students calculate a 2-dimensional Fourier transform, in order to learn that the phase oscillates only parallel to the shift vector.
Combine the 2-D Fourier with a change of length and direction of the shift vector.