Interactive guide to diffraction ..

Interactive Tutorial about Diffraction
Powder diffraction: powder pattern

Powder diffraction
Few crystals
Powder pattern
Preferred orientation
Pair distribution function

Interactive examples
PDF simulator

As seen in the last section, the individual diffraction patterns of the individual powder grains add up to the corresponding 2-dimensional diffraction pattern. Usually a powder diffractometer does not record the 2-dimensional diffraction pattern. Instead it records the intensity at intervals of constant THETA. In the two dimensional pattern this corresponds to the intersection of the two-dimensional plane with the Ewald sphere. This corresponds to a circle of radius 1/lambda that touches the origin of reciprocal space. Lets assume that lambda is very short and the circle will be close to a straight line.

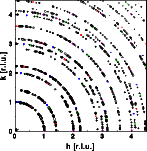
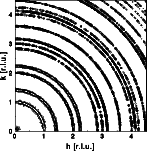
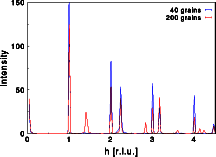
The left image above shows again the 2D diffraction pattern obtained from 40 grains. The corresponding trace along [h00] shown in the right image (blue curve) is quite different than we would have guessed. Some lines are completely missing. Our diffraction pattern was recorded with a stationary sample of 40 powder grains. These are too few grains to evenly cover the powder rings. The trace, cut at an arbitrary direction, suffers from insufficient statistics. In order to record a proper powder pattern, the sample should be rotated or more grains should be added. The middle image shows a 2D diffraction pattern obtained from 200 grains. The corresponding 1D trace along [h00] (red curve) shows a much better representation of the intensities. Still some of the reflections do not show the correct intensity.