Reciprocal space I: Reciprocity of distances

Reciprocal space
Reciprocity
Square lattice
Rectangular lattice
Oblique lattice
Translation of lattice
Rotation lattice
Interactive examples
2D crystal builder
Planes and HKL's
Finite size effect
Goto
Contents
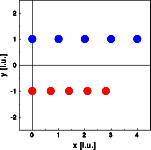
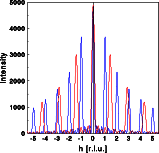
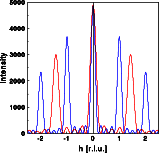
The right two images show the effect of changing the real space distance. Both images show a one dimensional cut through reciprocal space parallel to the row of atoms, once far into reciprocal space and once with high resolution. In both images the blue curve corresponds to the blue atoms above and the red curve to the red atoms respectively. The "Bragg" reflections of the red diffraction pattern are further apart than the blue ones, the red separation is 10/7 the blue separation. By decreasing the real space distances, reciprocal space distances increase.
Note, that this scaling holds for all features in reciprocal space, not just the "Bragg" reflections. This reflects the general principal of Fourier transforms that linear scaling in one space corresponds to the inverse scaling in the other space. The intensity of the "Bragg" reflections, however, does not follow the scaling. Instead the intensities decrease as the diffraction pattern is expanded, a feature we will explain in detail in the section on convolutions and modification of a structure.