ISP 205, Section 3 Hufnagel & Stein

UNIT I: THE SKY

OUTLINE

* Introduction: Tour of the Universe
* A. Scientific Models or Theories
* B. Appearance of the sky
* C. Models of the Solar System
* D. Motion and Gravity

Introduction: Tour of the Universe

Reading: Chapter 1

A. Scientific Models or Theories

Reading: Chapter 2 (sections 2.2, 2.3)

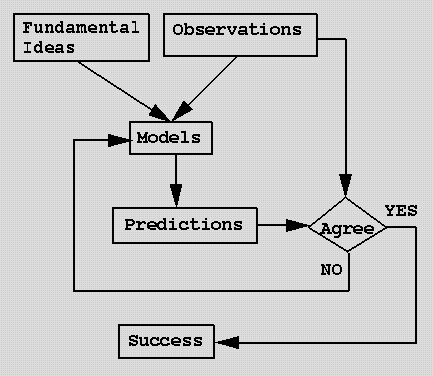
Model or Theory is a picture in your mind of reality

Goal:
Simplest rule to explain most phenomena
Scientific Models (Theories, Laws):
Isolate relevant experience from distracting or trivial effects
Discern a stable relationship in the flux of events
Express the relationship mathematically.
  1. Process of model building: (similar to everyday problem solving)
    1. Problem
    Observations to explain or conflict between observations and existing model
    Define what problem is. Ask the right questions.
    2. Generate a New Model/Theory
    Use divergent, flexible thinking; brainstorming.
    More than one possible solution, weigh pros and cons.
    Usually modify old model, occasionally something entirely different.
    based on fundamental ideas, previous theories, aesthetics and solution to problem
    3. Test Model/Theory
    Make Predictions
    Compare predictions of model with new observations.
    How well does model correspond to reality?
    Revise model/theory if necessary (-> step 1).
    [video: magic hut (start 3m54s)(20 min)]

  2. Criteria for Fruitful, Successful Model

  3. Limitations
    Models are based on limited experience. They are extrapolated to a range of similar situations and are applied in a broader context than that in which they were developed. Sooner or later, enough contradictory observations exist that the assumptions are no longer valid. Theories are seen to be too limited or too inaccurate.
    Examples:

  4. Proof
    Can disprove a theory by failure to correctly predict phenomena. Cannot prove a theory correct. Scientists know that none of the theories and models we use are perfect:
    The criterion for a good model is its usefulness for the task for which it is used.
    Can increase our confidence in it by successes in predicting phenomena.

    Activity: surviving in the wilderness

B. Appearance of the sky - what do we see?

Reading: Chapter 4

  1. Model of Sky -- Celestial Sphere

    Reading: sections 4.3, 4.4

    Problem: location of stars, motion of planets, what holds stars up
    Model: Celestial Sphere
    ancient - stars on crystal sphere
    modern - globe surrounding Earth
    Celestial Equator - over Earth's equator, = projection of Earth's equator
    Celestial N & S Poles - over Earth's poles, = projection of Earth's poles
    zenith - point directly overhead
    meridian - line from north celestial pole through zenith to south point on horizon.
    [AST disk, celestial equator 9998, Earth 10002, meridian 10003-4]
    Use: Coordinate system
    Declination - angle N or S or celestial equator (like latitude), measured in degrees
    Right Ascension - East-West position on celestial sphere (like longitude). Measured eastward from position where sun crosses celestial equator in spring (vernal equinox), in units of hours:minutes:seconds.
    [AST disk: 9983(?), 9995-10000]
    [demo: celestial globe]
    Twelve Constellations in the Zodiac.
    Pisces (S of Pegasus, see in fall) (RA 0 h)
    Gemini (near Orion, see in winter) (RA 6 h)
    Virgo (near Leo, see in spring) (RA 12 h)
    Sagittarius (S of Vega, see in summer) (RA 18 h) Sept. Sky Map from Abrams Planetarium

    Limitations:
    All models have limitations.
    Need different models for different purposes.
    Limitation of Celestial Sphere Model: Third dimension - distance.

  2. The Sun

    Reading: sections 4.4, 4.5

    (i) Daily Motion, due to Rotation of Earth toward the East on its axis
    E->W re. horizon
    Time: day determined by rotation of Earth.
    [star trails, AST disk 9931, 10070-71]
    [Rotating telescope represents Earth, AST disk, step 10090-10105, slow play 10106-10166]
    Demo: spotlight and globe
    [Rotating Earth from geosynchronus orbit, AST disk, step 11155-11188]
    demo: voyager

    (ii) Annual Motion, due to orbit of Earth toward East about Sun
    W->E re stars.
    Path of sun in sky = ECLIPTIC
    Seasons: Due to inclination of Earth's axis of rotation with respect to plane of its orbit around sun
    Year determined by motion of Earth around sun.
    Winter Solstice - about Dec 21. Sun farthest south, rises SE, sets SW. Long night, short day.
    Vernal (spring) Equinox - about March 21. Sun rises E, sets W. Equal day and night.
    Summer Solstice - about June 21. Sun farthest north, rises NE, sets NW. Long day, short night.
    Autumnal Equinox - about Sept 21. Sun rises E, sets W. Equal day and night.
    Demo: Motion re stars, spotlight and globe (move Sun then Earth, eg geo vs helio centric)
    Demo: light on liquid crystal, dependence of heating on inclination.
    [Height of Sun, AST disk 10180-10224]
    [slide sequence: sunrise Jan-June]
    [Inclination, AST disk 9921,9923-24(solar rays)]
    [AST disk 10168-79]
    Demo: voyager

  3. Stars

    Reading: sections 4.3, 4.6, 4.9, 4.10, Appendix chapter 4

          (i) Recognize Bright stars and their constellations.
          Locate on star map and in sky.
          16 Brightest Northern Hemisphere Stars
          Map of Taurus
      (ii) See different stars at different seasons, 
          because of Earth's orbit about the Sun.
          Night side of Earth faces in different directions.
      Planetarium, star maps
  4. Moon

    Reading: sections 3.1-3.3, 4.7

    Daily Motion
    Monthly motion: due to orbit of Moon toward East about Earth
    Time: month determined by motion of moon around Earth.

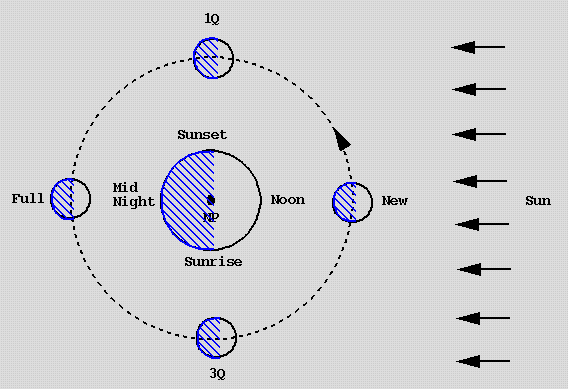
    (i) Phases
    Illuminated side faces sun. View it from Earth, see different fraction of illuminated side depending on position in orbit.
    Times of rising and setting at different phases.
    [Earth, Moon, Sun diagram, AST disk 9940, phases 9941-9949]
    Activity: spotlight, tennis and Ping-Pong balls

    (ii) Eclipses
    Solar - moon between sun and Earth, casts shadow on Earth
    Lunar - Earth between sun and moon, casts shadow on moon
    Moons orbit tilted 5o from the ecliptic. Twice a year point where moons orbit crosses ecliptic located on line between sun and Earth, so sun, moon and Earth can lie on straight line
    [Video: July 91 eclipse.]
    [Solar, AST disk 9965-71]
    [Lunar, AST disk 9958, 9960-64]
    [Earth, Moon, Sun diagram, AST disk 9957]
    Activity: spotlight, balls

  5. the Planets

    Reading: section 4.8

    Daily motion - East with respect to the horizon
    Annual motion - generally East with respect to the stars, near the ecliptic.
    Retrograde motion - part of each year moves West with respect to the stars
    [retrograde motion Mars: AST disk 9904, slow play 10277-10288]
    Demo: voyager
    Planetarium

    Venus & Mercury - always near Sun
    Mars, Jupiter and Saturn - anywhere along ecliptic
    Brightness not uniform - constantly changing
    Motion not uniform - faster and slower compared to the stars

  6. Planetarium

    Orientation: N,S,E,W
    planetarium, streets, equator, poles
    Motion of planets re stars,
    direct and retrograde motion
    Geocentric & Heliocentric views - Orrery
    [Activity: path of Mars re stars]

    Daily Motion
    Annual Motion (Stars, Sun)
    Moon
    Bright Stars and Constellations
    Coordinates
    [Activity: identifying stars on map, locate Moon]

C. Models of the Solar System

Reading: chapter 5

  1. Ptolemaic Model

    Reading: sections 5.1, 5.2

    Observations: daily and annual motions of the Sun, Moon, and planets. Eclipses. No stellar parallax.
    Fundamental ideas: Heavens are perfect. Perfect geometry is circle and spheres.
    Problem: predict planetary positions and motion
    Model: Geocentric. - Sun, Moon and all planets move around the Earth on circles.
    Natural motion of heavenly bodies is Uniform Circular Motion
    Observed motions can't be explained by simple geocentric model, need complex model of epicycles, eccentric and deferent
    Deferent - Daily motion E-> W, and Motion W-> E re stars
    all heavenly objects whirl around Earth E->W daily.
    Planets move slower along deferent than stars
    Epicycles - Retrograde motion
    Planet moves around epicycle, center of epicycle moves along deferent.
    When planet is moving backwards along inner part of epicycle ->retrograde motion
    Venus and Mercury
    Centers of epicycles lie on Earth-sun line.
    Size of epicycles determined by greatest distance from sun.
    Mars, Jupiter and Saturn
    Radius of epicycles align with Earth-sun radius in order to make retrograde motion occur when planet opposite the sun, but anywhere on deferent.
    Size of epicycle determined by size of retrograde loop. Decreases from mars -> Jupiter -> Saturn.
    Eccentric - Non-uniform motion
    Earth offset from center of deferent circle.
    Planets appear to move faster when closer to Earth, slower when farther away
    Equant - non-uniform motion
    motion along deferent not uniform. Appears uniform when viewed from point offset from center of deferent opposite to eccentric

    [Diagram, AST disk 6979, detail 6980, book plate 9906, diagram 9907]
    [Geocentric view, AST disk, side 2, chapt 32]
    [Deferents & epicycles, Mechanical Universe prog 9, chapt 18, Almagest chapt 19]
    [Ptolemaic and Tychonian models, Mechanical Universe, prog 21, chapt 8 (15131)]
    Tests:
    Predicted planetary positions and motions. Accurate to a few moon diameters. Tycho Brahe upset that predicted conjunction of Jupiter & Saturn off by a month.
    No observable parallax. Earth doesn't appear to move.
    The geocentric model explains all the basic motions and observations made with the naked eye.

  2. Copernican Model (1473-1543)

    Reading: sections 5.3, 5.6, 5.7

    [Portrait, AST disk 6995,6]

    Observations: Same as before: daily and annual motions of the Sun, Moon, and planets. Eclipses. No stellar parallax.
    Fundamental ideas: Sun is at center. Perfect geometry of circles and spheres.
    Problem:
    Aesthetics - Ptolemy did not use uniform circular motion (equant)
    Model: Heliocentric - all planets, including Earth, orbit the sun.
    Planets closer to sun move faster
    Retrograde motion: faster moving inner planet overtakes and passes slower moving outer planet.
    [AST disk, diagrams 9912,13, model 6997, book 6998]
    [Geocentric view, AST disk, side 2, chapt 33]
    [Copernican model, Mechanical Universe, prog 21, chapt 9-10 (17000, 17141-17190)]
    Tests:
    Accuracy of predicted planetary positions unchanged.

    Problems:
    Why do objects fall straight down on spinning Earth?
    How are atmosphere and moon carried along by moving Earth?
    Galileo observed moons of Jupiter carried along with Jupiter
    No parallax (stars very distant, parallax very small, first observed by Bessel in 1838)
    [AST disk 7032].
    Video: Mechanical Universe, program 4, chapter 19 (How things fall)
    [parallax, AST disk: 9918]

    Violent arguments
    Appeal -
    Aesthetic: Simple natural explanation of retrograde motion - inner planets move faster, so overtake outer planets. Explains why always at opposition. Symmetry of nested orbits.
    More universal, Earth like other planets.
    Repugnance -
    Earth not unique
    Resolution - New Observations
    Phases of Venus -> Venus orbits sun (Galileo, 1565-1642) [portrait, AST disk 7025,6] [Robbins et al. Fig 5-19.]
    Sunspots, moon mountains -> heavens not perfect
    Tycho Brahe (1546-1601) observed new bright star in Cassiopeia (supernova).
    Showed no parallax -> so farther than moon -> star -> stars change;
    Observed comet, showed crossed orbits of Jupiter and Mars, so no crystal spheres.
    [Portrait, AST disk 7004,5, observatory 7008, instruments 7012, slides of Hven]
    Stellar parallax observed 1838 (Friedrich Bessel 1784-1846)

    Philosophy - Earth not unique! Revolutionary! (Origin of meaning of word is name of Copernicus book, "On the Revolutions of the Heavenly Spheres")

  3. Keplerian Model (1571-1630)

    Reading: section 5.4

    [portrait, AST disk 7019,20]

    Observations: Tycho Brahe's observations of Mars and other planets
    Problem:
    Observations of planetary positions by Tycho Brahe (1546-1601) much more accurate ( ~1/8 moon diameter). Inconsistent with Copernican model.
    [conflict observations and models, Mechanical Universe, prog 21, chapt 2 (4500)]
    Model:
    a. Elliptical planetary orbits
    b. Non-uniform speed around orbit
    c. P2(yr) = a3(au), planet's period is related to its distance from sun
    [ellipses, Mechanical Universe, prog 21, chapt 3-4]
    [diagram, AST disk, 9914,5]
    [3 laws, Mechanical Universe, prog 8 22, 25 (3 laws)]
    [Mechanical Universe, prog 21, chapt 12 (Earth's orbit), 13,14 (Mar's orbit)]
    Tests:
    Derived for Mars, test with other planets and comets.
    Much more accurate predictions of planetary positions.
    Philosophy:
    Non-uniform planetary motion. Not natural motion. Need a force.
    Appeal:
    Accuracy.
    Universality - all orbiting bodies (planets and satellites) have same properties.

  4. Comparative Summary of Solar System Models

D. Motion and Gravity

Reading: section 5.5

Ptolemy, Copernicus and Kepler's models were descriptive and geometric. They did not explain. Newton developed an explanation.

[Newton portrait, AST disk 7034]

  1. Newton's Law of Motion (1642-1727)

    Motion only with respect to something
    Velocity
    Speed=distance traveled in given time
    Velocity=speed in given direction=distance traveled in given direction in given time
    distance = velocity x time (e.g. mi/hr x hr = mi)
    Acceleration=change in velocity in given time
    speed up, slow down, turn
    Acceleration is intrinsic, need refer to nothing else.
    [Inclined planes, Mechanical Universe, program 4, chapt 25-26]

    Newton's Law of Motion

    acceleration = force / mass

    Force = push or pull
    Mass = inertia, resistance to change of motion. Depends on amount of matter, not size.

    Examples: cars, balls, rockets
    Demo: pucks on air table
    Demo: pull cart with weights using spring
    Orbital Motion: direction changes (speed also changes slightly) -> need force!
    [velocity, acceleration and force, Mechanical Universe, program 6, chapt 13 (good animation)]
    Example: cars turning corners

  2. Newton's Theory of Gravity

    Planet's motion in its orbit is accelerated (direction and magnitude of velocity changes). Force is needed. Newton said force is gravity:

    Source of Gravitational Force is Mass.
    Every object attracts every other object by force of gravity.
    More Mass -> stronger gravity.
    Larger Distance -> weaker gravity.

    Fgravity = G M m / D2

    [AST disk: F toward center 7087, F on planet 7088]
    [Mechanical Universe, program 8, chapt 28-29 (force of gravity)
    Show: Ratios and Exponents
    Interactive Physics II (PC): falling, orbiting bodies with Motion Activity
    Tests
    Acceleration of Moon. (Know acceleration = F/m at Earth's surface, Know distance to Moon, Calculated acceleration at Moon's distance, Compare actual acceleration found from period and distance) [Mechanical Universe, program 8, chapt 38-43, Newton's prediction 40; Moon's acceleration 41-42; circular motion, a=v2/r, prog 9 chapt 21-26]
    Solved problems of Copernican system: objects fall straight down, atmosphere stays with planet, moon stays with planet [Mechanical Universe, prog 4, chapt 34-36, (falling ball)]
    Orbits of comets, spacecraft, Neptune and Uranus. (Laplace 1800 calculated Uranus orbit)
    Derivation of Kepler's laws. Used to determine masses.
    Discrepancy: Mercury, high speeds
    Philosophy:
    Mechanical Universe.
    Given knowledge of where everything is and how it is moving now, and enough computer power, you can calculate everything that will happen in the future.
    Appeal:
    Universal -- all motion, terrestrial as well as celestial
    Accurate predictions.
    Aesthetic -- simple, few assumptions
    Application: Determining masses
    Can only determine masses of astronomical bodies where there are at least two bodies orbiting around each other.
    Can measure line of sight velocity by Doppler shift
    Can measure period
    Derivation of Kepler's Third Law (optional)
    Start with Newton's equations of motion and gravity
    a = F/m and Fgravity = GMm/D2
    Substitute Fgravity for the force in the equation of motion.
    a = GMm/D2 * 1/m = GM/D2
    (Note: acceleration independent of mass of accelerated body)
    a = change in velocity / time = v/t
    v = distance / time = D/t
    a = D/t2
    D/t2 = GM/D2
    Solve for M: multiply by D2 and divide by G
    M = D3/Gt2 (Kepler's Third Law)
    Kepler's Third Law in Solar System Units
    is
    M1 [Msun] + M2 [Msun] = D[AU]3 / P[yr]2
    where
    M1 = mass of body 1, in units of mass of Sun
    M2 = mass of body 2, in units of mass of Sun
    D = radius of nearly circular orbit (= semi-major axis of ellipse in general) in AU (Astronomical Units)
    P = period of orbit in years
    Must convert distances to AU
    Must convert times to years
    If given other information must determine Distance and Period
    e.g. d=vt, t=d/v, where here distance = circumference of orbit not its radius.
    If one mass is much less than the other, it can be neglected.
    Work problem in class.
    Reading: p 87, sec 15.5, p 439

  3. Energy

    Reading: page 107 (section 6.5)

    Energy = ability to do work
    Kinetic energy = energy of motion
    Potential energy = work a force could do
    Energy is conserved:

    Kinetic Energy + Potential Energy =Total Energy = constant

    1/2 m v2 - GMm/D = E = constant

    ETotal = 0 at infinit separation. As fall the KE increases (speeds up), so the PE must decrease (become more negative) to keep the total energy = 0 (constant).

    Demo: pendulum
    If Energy is conserved, how do things get started, or once moving how do they step? Work transfers energy.
    [Video: Ring of Truth: Change 2297-3412 (Toure de France, energy conservation)]
    Applications:
    Do work to change speed, not to turn
    Bound orbit: total energy < 0.
    Unbound orbit: total energy > 0.
    Escape velocity: speed required to escape to infinity.

  4. Einstein's Theory of Motion and Gravity (Optional)

    Reading: section 19.4

    Problem:
    Speed of Light the same for all observers.
    orbit of Mercury: axis precesses
    All objects fall at same speed: inertial mass = gravitational mass
    Demo: air track
    Video: Mechanical Universe, program 25, chapter 25-27
    New Model:
    Laws of Physics the Same for all freely moving observers.
    Speed of Light the Same for all observers.
    Can Not Distinguish between Gravity and Constant Acceleration by some other force.
    Predictions:
    Light is attracted by gravity: Bending of Light by the Sun Video: Mechanical Universe, program 25, chapter 29
    Energy = Mass (E=mc2): move faster -> more energy -> more mass
    -> more inertia, can't exceed the speed of light
    Time dilation -- time slows down when moving
    Gravity is Geometry: Mass warps space-time. Warped space-time controls how objects move.
    Tests:
    Orbit of Mercury, lifetimes of cyclotron particles, displacement of stars close to Sun, increase of inertia as speed increases.
Links to other resources on the Sky
* Abrams Planetarium
* Knowing the Sky (UCSD)
* The Constellations and their Stars (UWisc)
* The 26 Brightest Stars (UWisc)
* Purchasing Amateur Telescopes FAQ (NWestern)
This page has been accessed times.

Updated: 1997.03.31 (Monday) 09:19:32 EST
Visions of the Universe

Beth Hufnagel's home page, email: bhufnage4@pilot.msu.edu
Bob Stein's home page, email: steinr@pilot.msu.edu