

When to use Kirchoff's laws
Although Kirchoff's laws were used to derive the simple relations for adding resistors in series and parallel, not all problems can be broken down into such simple pieces. Below are three diagrams which may need to be solved (e.g. given the resistances and voltages of the batteries, find all the currents).

The left-side figure can be treated by breaking up the circuit into pieces and applying the rules for adding resistances in parallel and series. The resistors R3, R4 and R5 can be treated as a single resistor with resistance R345, which can then be added in parallel with R2, to give an effective resistance R2345. The battery sees a net resistance R = R1 + R2345.
The middle and right-side figures can not be solved by such a strategy. Instead, one must write down Kirchoff's laws then solve the equations.
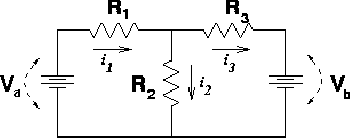 For
instance consider the right-side figure. The 3 currents
through the 3 resistors i1,
i2
and i3
are unknown. The three unknowns can be found by solving 3
equations: For
instance consider the right-side figure. The 3 currents
through the 3 resistors i1,
i2
and i3
are unknown. The three unknowns can be found by solving 3
equations: |
The first equation describes current conservation into the the node. Note that i1 is defined as flowing into the node (to the right) while i2 and i3 are defined as flowing out of the node (down and to the right).
The second equation expresses the requirement that voltage losses cancel voltage gains for the loop on the left.
The third equation expresses the sum of voltages around the right loop. Note that if one makes a counter-clockwise loop, one goes against the current through R3 and the sign of that term is therefore opposite the normal one.
Remember that one gains the voltage of the battery when travelling from the small hashes and leaving from the large hashes in the battery. One could also imagine writing equations for a third loop, that travels all the way around the circuit, through both batteries. However, such an equation is merely a linear combination of Eq. 2 and Eq. 3 above.