

Decay constants and half lives
Most nuclear decays occur independently (unlike those that occur in a chain reaction) where a given fraction of nuclei decay in a given time, independent of the number of nuclei. In a time Dt the number DN that decay are:
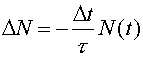
The number that have not decayed at time t is N(t) and t is the exponential decay time. It is termed "exponential" because the solution to the above equation is:
![]()
where N0 is the number of undecayed nuclei at t = 0. The symbol l = 1/t is known as the decay constant.
A half-life is the time it takes for half of the nuclei to disappear. At that point N(t) is one half of N0:
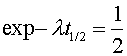
Taking the logarithm of both sides of the above equation, gives the half life t1/2 in terms of the exponential time t.
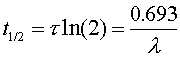
Working problems with exponential decays are good practice for many other fields. Exponential growth and decay are common concepts in biology, economics, and other sciences.