 Problem:
Problem:Examples for AC circuits
Problem:
A
n AC circuit carries an rms current of 7.0 Amps. The current travels through a 12 Ohm resistor. a.) What is the peak current? Solution: Multiply the rms current by sqrt(2). I = 9.90 A b.) What is the power dissipated in the resistor? Solution: You can use the normal formula, i2R, provided that you use the rms value of the current. 588 W c.) What is the peak voltage drop across the resistor?Solution:
Use Ohm's law, being careful to use the peak current to get the peak voltage. 118.8 V Problem:
Problem:
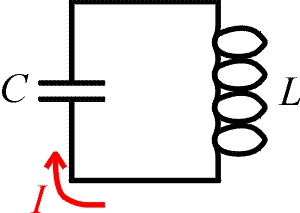
Consider the LC circuit to the right. If one needs to tune this circuit to a frequency of 84 kHz, and the capacitor has a capacitance C = 3.0 mF, what inductance L is needed?
Solution:
Use the relation, ![]() .
Solve for L.
.
Solve for L.
L = 1.20E-6 H
 Problem:
Problem:
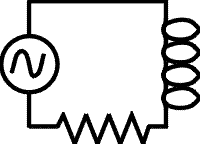
a.) What is the impedance of the circuit to the right if: f = 60 Hz, L = 20 mH, R = 4.0 W?
Solution: ![]()
Z = 8.54 W
b.) If the r.m.s. voltage of the source is Vrms = 110 V, what is the r.m.s. current?
Solution: Irms = Vrms/ Z
Irms = 12.9 amps
c.) What is the peak current?
Solution: Ip = sqrt(2) ·Irms
Ip = 18.2 amps
d.) What is the power dissipated in the resistor?
Solution: P = I2rms·R
P = 1320 W
Example #4
Problem:
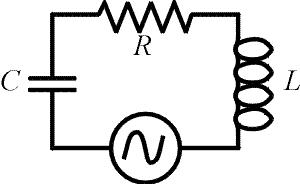 a.) What is the capacitance such that the current through the circuit is a
maximum?
a.) What is the capacitance such that the current through the circuit is a
maximum?
DATA: f = 60 Hz, L = 20 mH, R = 4.0 W, Vrms = 110 V?
Solution: Choose the capacitance such that the reactance of the capacitor cancels the reactance of the inductor:
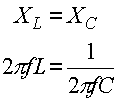
C = 8.8E-5 F
b.) What is the r.m.s. current through the circuit for the capacitance found in part a?
Solution: The impedance of of the circuit is determined completely by the resistor at resonance, Z = R. The current is then V/R.
I = 27.5 Amps
c.) Find the capacitance to make the impedance equal to 8 Ohms.
Solution: The impedance is:
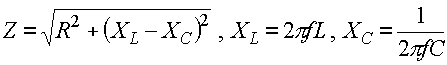
First solve for the reactance of the capacitor (Xc = .612 Ohms), then find C.
C = 4.33E-3 F