LRC circuits
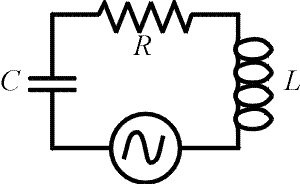 Here
we consider circuits with an AC power supply and all three fundamental elements: a
resistor, an inductor and a capacitor. The same current flows through each element at
every instant in time. The voltages across the four elements must sum to zero when
travelling around the loop at any instant as well.
Here
we consider circuits with an AC power supply and all three fundamental elements: a
resistor, an inductor and a capacitor. The same current flows through each element at
every instant in time. The voltages across the four elements must sum to zero when
travelling around the loop at any instant as well.
Although the voltages across all the
elements rise and fall at the same frequency, they do not all have the same phase.
When two signals have the same frequency but different phases, the sine waves
representing the signals begin oscillations at different times. There is an offset of the
patterns. For instance if we say one signal is 90 degrees behind another, that would mean
that the sine wave would be displaced by one fourth of a period.
A consequence of this is that the (rms voltage across the capacitor) +
(rms voltage across the inductor) + (rms voltage across the resistor) add
up to MORE (sometimes much more) that the rms voltage supplied
by the generator.
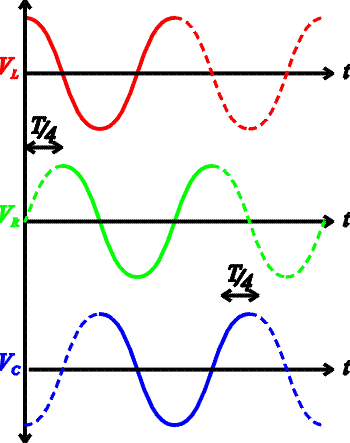 In
the figure on the right, the voltage drop across each element is shown as a function of
time. The green line, which is the voltage drop across the resistor, also demonstrates the
phase of the current. One can see that VL preceeds
the current by one fourth of a period. This is because the inductor's
voltage drop is
largest when the current is rising fast, since it is proportional to
DI/
Dt.
The opposite is
true of the voltage across the capacitor Vc , which
keeps rising until the current is no longer forward. This is because the
voltage on a capacitor is proportional to
the charge which grows as long as the current is positive. Thus VL
and Vc are 180 degrees out of phase, which
means they simply have opposite signs.
In
the figure on the right, the voltage drop across each element is shown as a function of
time. The green line, which is the voltage drop across the resistor, also demonstrates the
phase of the current. One can see that VL preceeds
the current by one fourth of a period. This is because the inductor's
voltage drop is
largest when the current is rising fast, since it is proportional to
DI/
Dt.
The opposite is
true of the voltage across the capacitor Vc , which
keeps rising until the current is no longer forward. This is because the
voltage on a capacitor is proportional to
the charge which grows as long as the current is positive. Thus VL
and Vc are 180 degrees out of phase, which
means they simply have opposite signs.
The impedance is the ratio of
the peak voltage of the source to the peak current. This impedance depends on the
frequency of the source as well as the values of L, C
and R. The impedance Z (derivation on next page) can be thought of as
the AC analog of resistance.
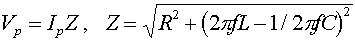
The impedance becomes a minimum (for a given
R) when the
reactance of the inductor,
XL = 2pfL,
is canceled by the reactance
of the capacitor XC = 1/(2
pfC).
This is the same resonant
condition that was given for LC circuits previously.
Examples
AC circuits index
Lecture index
 Here
we consider circuits with an AC power supply and all three fundamental elements: a
resistor, an inductor and a capacitor. The same current flows through each element at
every instant in time. The voltages across the four elements must sum to zero when
travelling around the loop at any instant as well.
Here
we consider circuits with an AC power supply and all three fundamental elements: a
resistor, an inductor and a capacitor. The same current flows through each element at
every instant in time. The voltages across the four elements must sum to zero when
travelling around the loop at any instant as well.
 In
the figure on the right, the voltage drop across each element is shown as a function of
time. The green line, which is the voltage drop across the resistor, also demonstrates the
phase of the current. One can see that VL preceeds
the current by one fourth of a period. This is because the inductor's
voltage drop is
largest when the current is rising fast, since it is proportional to
DI/
Dt.
The opposite is
true of the voltage across the capacitor Vc , which
keeps rising until the current is no longer forward. This is because the
voltage on a capacitor is proportional to
the charge which grows as long as the current is positive. Thus VL
and Vc are 180 degrees out of phase, which
means they simply have opposite signs.
In
the figure on the right, the voltage drop across each element is shown as a function of
time. The green line, which is the voltage drop across the resistor, also demonstrates the
phase of the current. One can see that VL preceeds
the current by one fourth of a period. This is because the inductor's
voltage drop is
largest when the current is rising fast, since it is proportional to
DI/
Dt.
The opposite is
true of the voltage across the capacitor Vc , which
keeps rising until the current is no longer forward. This is because the
voltage on a capacitor is proportional to
the charge which grows as long as the current is positive. Thus VL
and Vc are 180 degrees out of phase, which
means they simply have opposite signs.