Ampere's law
Ampere's law is a mathematical statement of the relationship between currents and the magnetic fields they generate. It is thus the magnetic equivalent of Gauss's law, which relates charges to their electric fields. Ampere's law is stated below for the sake of the curious, but it will not be necessary to use it in physics 232: the formulas we need for the B fields of solenoid and a long straight wire can instead be taken on faith.
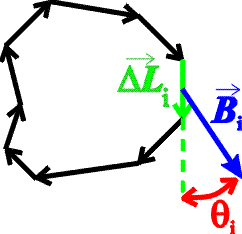
Ampere's law is defined in terms of an arbitrary surface and the closed loop that forms its boundary. It is thus reminiscent of Gauss's law, which involves a volume and the closed surface that forms its boundary. Consider a closed loop, not necessarily a circle, that is broken into small elements of length DLi with a magnetic field Bi at each element.

Ampere's law states that the sum over elements of the component of the magnetic field along the direction of the element, times the element length, is proportional to the current I that passes through the loop:
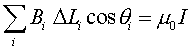
This is the general statement of Ampere's law. For the case of a wire, the loop can be a circle drawn around the wire, and since the field is then always tangent to the circle, cosq = 1. The circumference of the circle of radius r is 2pr, so Ampere's law gives
![]()
which is the expression for the magnetic field of a wire given before. Ampere's law will also allow us to calculate the magnetic field for a solenoid.