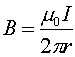 one can solve
for I.
one can solve
for I.Examples for Magnetic field sources
Example #1
Problem:
A magnetic field of magnitude 1.30E-3 T is measured a distance of 3.0 cm from a long straight wire. What is the current through the wire?
Solution:
Using 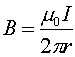 one can solve
for I.
one can solve
for I.
I = 195 amps (lots of current!)
Example #2
Problem:
a.) Two wires carry currents in the same direction as shown below. Where are the points where the magnetic field is zero?
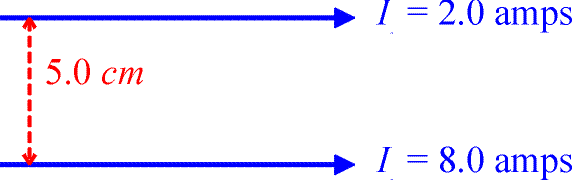
Solution:
Using the right-hand rule, will convince one that the magnetic field contriubtions from the two wires only cancel in the region between the wires. One must find a position that is four times closer to the upper wire, which would be one cm below the upper wire. Using algebra to come to the same conclustion, consider a point located a distance y below the upper wire.
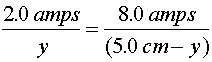
Solving for y gives the 1.0 cm answer.
1.0 cm below the upper wire
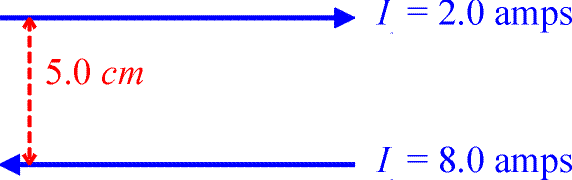
b.) Now consider two wires carrying currents in the opposite direction as shown below. Where are the points where the magnetic field is zero?
Solution:
Using the right-hand rule again, allows one to see that the magnetic-field contributions from the two wires have opposite signs either above or below the wires, but not between them. Of course when you are below the lower wire, the upper wire can never cancel out the lower wire's contribution since the lower wire carries more current and is closer to you. Therefore consider a point a distance y above the upper wire.
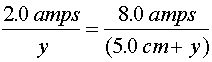
Solving for y,
1.67 cm above the upper wire
Example #3
Problem:
What is the force felt by the square loop shown below due to the current in the long wire?
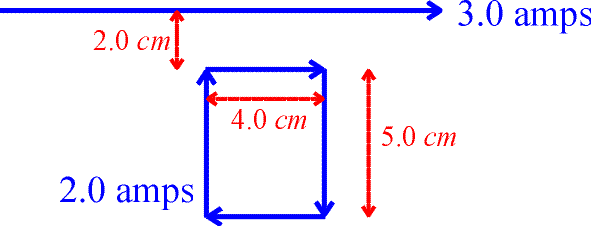
Solution:
There is no net contribution from the two vertical segments
of the rectangular loop since the currents are in opposite directions. Using 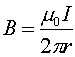 with r = 2.0 cm and
= I = 3.0
amps, one can solve for the magnetic field at the upper segment of the rectangular loop
due to the long wire. One can then find the force on the upper segment, F =
ILB,
with L = 4.0 cm and I
= 2.0 amps. The force on the upper
segment is upwards toward the long wire because the currents are in the same direction.
Repeating the steps for the bottom wire which is located a distance r
= 7.0 cm from the long wire, allows one to calculate the force on the lower
segment or the rectangle. This force points down, but is obviously smaller in magnitude
than the force on the upper segment. Adding the forces gives the answer.
with r = 2.0 cm and
= I = 3.0
amps, one can solve for the magnetic field at the upper segment of the rectangular loop
due to the long wire. One can then find the force on the upper segment, F =
ILB,
with L = 4.0 cm and I
= 2.0 amps. The force on the upper
segment is upwards toward the long wire because the currents are in the same direction.
Repeating the steps for the bottom wire which is located a distance r
= 7.0 cm from the long wire, allows one to calculate the force on the lower
segment or the rectangle. This force points down, but is obviously smaller in magnitude
than the force on the upper segment. Adding the forces gives the answer.
F = 1.71E-6 N
Example #4
Problem:
A long cylindrical solenoid with 200 turns/cm carries a current of 4.0 amps. The diameter of the solenoid is 0.4 cm and the length is 8.0 cm and the mass of the moon is 7.35E22 kg. What is the magnetic field inside the solenoid?
Solution:
The magnetic field only depends on the current (I = 4.0 amps) and the number of turns per unit length (N/L = 200).
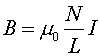
B =0.1005 T