Examples for induction
Example #1
Problem:
An airplane moves such that its velocity and wingspan are both perpendicular to a magnetic field of 1.0E-4 T. How fast must the plane move to generate a potential difference of 12 V between the wing tips? (DATA: wingspan=36.0 m.)
Solution:
V = v L B, put in the numbers and solve for v.
v = 3.3E3 m/s
Example #2

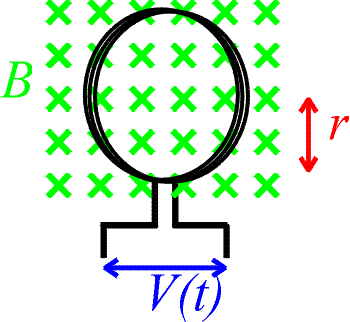
Problem: Consider the loops shown above. A magnetic field of 0.5 T is introduced into the loop over a time t. If the radius of a loop is 4.0 cm and there are 600 turns, how quickly (find t) must the field be introduced to attain a 12 V potential?
Solution:
Use Faraday's law:
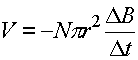
The change in the magnetic field is 0.5 T and everything else is given, so solve for Dt which is the time over which the field is introduced t.
t = 0.126 s
Example #3
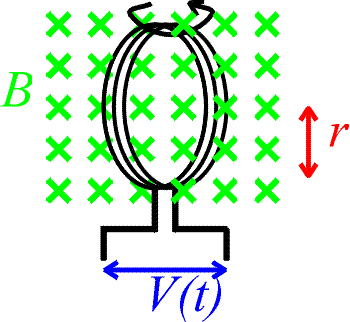
Problem: Consider the loops shown above which are immersed in a constant magnetic field of 0.5 T. The radius of the loop is 3.0 cm. If the loop is rotated at 60 Hz, how many turns are needed to achieve an r.m.s.voltage of 110 V?
Solution:
The rate of change of the flux is
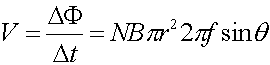
We want an r.m.s. voltage, which is the maximum voltage times 1/sqrt(2).
N = 292
Example #4

Problem: Consider the transformer shown above. The r.m.s. voltage of the primary source is 110 V, and there are 100 turns in the primary loop compared to 500 turns in the secondary loop. What is the power consumed in the 10 W resistor?
Solution:
The voltage of the secondary source is (500/100) times larger, Vs = 550 V. The power is Vs2/R.
P = 30.25 kW
Example #5
Problem:
a.) Consider a solenoid which has zero current at t = 0, and is then ramped up to 2.0 amps in 1.5 ms. If the voltage across the inductor during this time is 14 V, what is the inductance of the solenoid?
Solution:
Use V = L DI / Dt to find L.
L = 0.0105 H
b.) What is the final energy stored in the solenoid?
Solution:
Use U = (1/2) L I2 to find U .
U = .021 J
Example #6
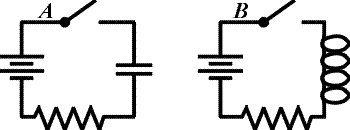
Problem: Consider the two circuits, A and B above. The switches are closed at time t = 0 after being open a long time.
1.) Which circuit(s) have a current in the instant immediately after t = 0 ?
2.) Which circuit(s) have a current a long time after t = 0 ?
3.) Which element(s) (aside from the battery) store energy a long time after t = 0 ?
A, B, both the inductor and capacitor.
Example #7
Problem: Consider an inductor created by coiling N turns of wires around a cylinder of radius R and length h. The inductance is measured to be 0.025 H.
1.) What happens to the inductance if the length is doubled?
2.) What happens to the inductance if the number of turns is doubled?
3.) What happens to the inductance if the radius is doubled?
The inductance is (halved to 0.0125 H, quadrupled to 0.1 H, quadrupled to 0.1 H)