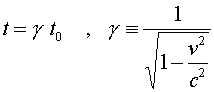
Time dilation
The fact that the speed of light is the same in all reference frames has the consequence that moving clocks run slow. This means that if two events occur at the same place, such as the ticks of a clock, a moving observer will measure the time between the events to be longer. The relation between a time measured by a stationary observer t0 to the time t measured by an observer moving with velocity v is:
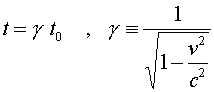
The gamma factor appears often in relativity. It is always greater than unity, but very close to it for small velocities. (If the velocity were greater than c, gamma would be undefined; but that never happens, as we will see shortly.)
This result can be shown to result from the two fundamental postulates by considering a light clock. This imaginary clock would work by ticking every time a light pulse reflected back to the lower mirror as shown below.
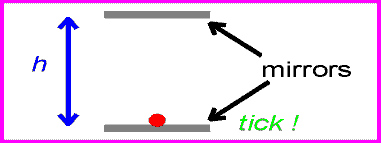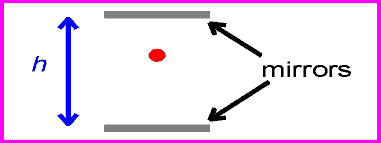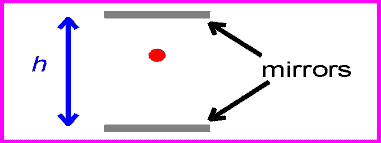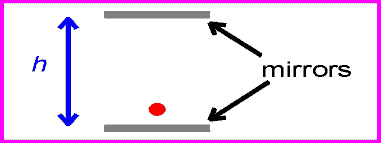
The time between ticks and tocks for the stationary clock is:
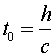
One can now view the same clock as it moves past with velocity v.
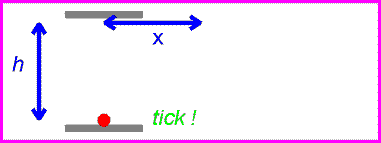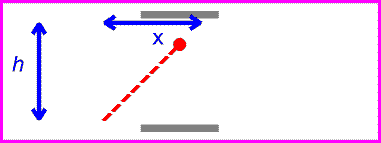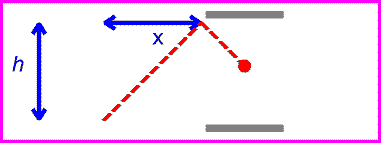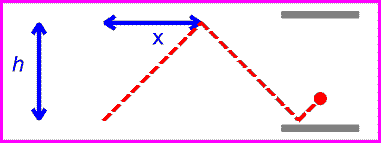
The time between ticks and tocks is again given by the distance traveled by the red pulse divided by c.
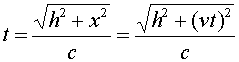
Solving the above equation for t in terms of h, v and c gives
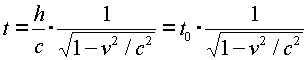
Thus the moving observer sees a longer time by the factor g defined above.
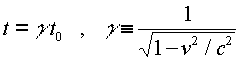
We derived the time dilation effect using a very simple clock; but the result applies equally to all clocks, including complex ones such as decaying radioactive particles or even biological systems. It is therefore better to think of the effect as an unexpected truth about space and time, rather than as a property of the clock. In any case, the effect is NOT caused by forces operating on the clock---since as you know, NO force is required to keep an object moving at constant velocity.